Lab 13 - Electrochemistry and the Nernst Equation
Goal and Overview
A voltmeter is used to study the relative reduction potential of various metals and the concentration dependence of voltage in concentration cells. The solubility of silver halides will be determined by measuring the voltage of a saturated solution against a standard solution of Ag+ ions. From the solubility, the values ofKsp
for AgCl, AgBr, and AgI will be calculated.
Objectives and Science Skills
-
•Understand and explain the chemistry, components, function, and operation of electrochemical and concentration cells.
-
•Construct electrochemical cells and measure E0cell for different pairs of metals and metal ion solutions; identify anode and cathode and explain what occurs at each (oxidation or reduction).
-
•Construct concentration cells and measure Ecell values; use experimental values to calculate Ksp for slightly soluble silver halide salts.
-
•Quantitatively and qualitatively compare experimental results with theoretical values.
-
•Identify and discuss factors or effects that may contribute to the uncertainties in values determined from experimental data.
Suggested review and external reading
-
•relevant reference information and/or textbook information on thermodynamics, electrochemistry, equilibrium, and free energy
Background
The primary measurement in electrochemistry is the voltage (V) of an electrochemical cell. The voltage describes the relative energies of electrons on different atoms and/or ions. The energy difference, or potential difference, between two electrons is measured in volts (joules/coulomb). The electrons may be on two ends of a wire, on two atoms, or on the cathode and anode of a battery having a potential difference. An oxidation-reduction or redox reaction is a chemical reaction in which one or more electrons from one molecule or atom are transferred to another. Thermodynamics can predict if electrons would prefer to be transferred from one species to another based on the free energy change of the system. For example, electrons are more stable on copper than zinc, so if a piece of zinc is placed in a copper ion solution, the electrons will spontaneously transfer from Zn to Cu2+, where they are more stable.( 1 )
Zn(s) + Cu2+ → Zn2+ + Cu(s)
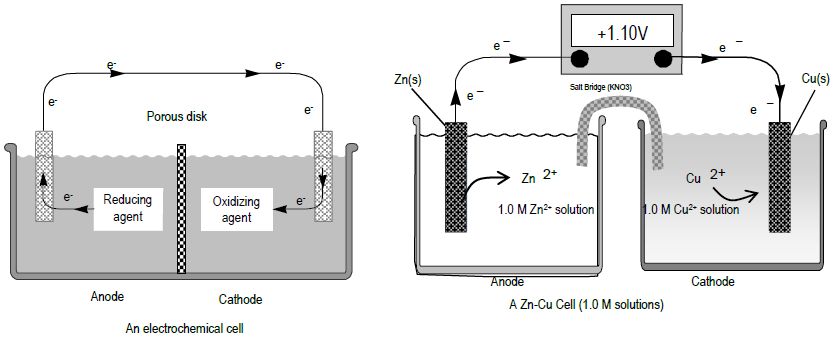
Figure 1
( 2 )
ΔG = ΔG° + RT ln Q
( 3 )
ΔG = −nFE, or E = −ΔG/nF
( 4 )
F = 96,485
= 96,485
 |
| coulomb |
| mole e− |
 |
 |
| Joule |
| mole − volt |
 |
ΔG = −nFE, or E = −ΔG/nF
this implies spontaneity is associated with a positive E.
If Eqs. 3ΔG = −nFE, or E = −ΔG/nF
and 4F = 96,485
= 96,485
 |
| coulomb |
| mole e− |
 |
 |
| Joule |
| mole − volt |
 |
ΔG = ΔG° + RT ln Q
(RT / nF × ln Q).
( 5 )
E = E° −
ln Q
| RT |
| nF |
2.303 log10 x = loge x = ln x).
( 6 )
E = E° −
log10 Q
| (0.0591 volts) |
| n |
Q = 1.
The value 0.0591 is the same for all cells at 25°C.
E° is also related to the electron energy differences of the oxidation and reduction reaction.
( 7 )
E°(cell) = E°1/2(reduction) − E°1/2(oxidation) = E°1/2(cathode) − E°1/2(anode)
E = 0
in Eq. 6E = E° −
log10 Q
| (0.0591 volts) |
| n |
( 8 )
E° =
log10 Keq
| (0.0591 volts) |
| n |
Procedure
Please use small volumes of solution to reduce the cost of buying chemicals and the problems with waste disposal. Dispose of all waste as instructed. Waste solutions must be segregated according to type. Read the labels on the waste bottles carefully. Clean up all spills. DO NOT THROW ELECTRODES AWAY. Please return them CLEAN. Please dispose of the used vials and salt bridges in the solid waste container in the back hood. Wash your hands thoroughly and carefully when done. If you do not dispose of waste correctly, you may lose points.Part 1: Determinations of E° for Metals vs. Copper
For the redox reactionA(s) + B2+  A2+ + B(s)
A2+ + B(s)
the Nernst equation is shown below.
 A2+ + B(s)
A2+ + B(s) ( 15 )
E = E° −
log10 Q = E° −
log10
| (0.0591 volts) |
| n |
| (0.0591 volts) |
| n |
 |
| [A2+] |
| [B2+] |
 |
To create a voltaic cell:
1
Fill two vials about 2/3 full of the solutions you will use, labeling each one before you fill it. Dry the outside of the vials if needed. Use only the dropper provided for filling your vials.
2
Put the two vials on the base of a ring stand, side by side in the jaws of a utility clamp, so they are held together.
3
The two liquid levels should be exactly the same to prevent siphoning of liquid from the higher level vessel into the lower. Arrange the vials in the clamp to level them if they are slightly different.
To create the salt bridge:
4
Use a strip of filter paper as instructed by your TA.
5
Fold the paper in half.
6
Holding the paper in tweezers, soak it in a small beaker containing 1.0 M KNO3.
7
Gently blot the strip on a Chem-Wipe. You don't want the concentrations of your solutions to be contaminated by solution from the salt bridge.
8
Put one end of the strip into the solution in one vial and the other end in the solution in the other vial.
Do not let the tweezers touch the liquid in either vial.
9
Clip one Cu wire electrode to one lead of the voltmeter; clip the other to other lead of the voltmeter.
10
Insert the electrodes into the solution of their own ion carefully so they do not touch the salt bridge above the surface of the solution. You can use the electrodes to push the filter paper strip out of the way.
11
Measure the voltage difference and the cell polarity with the digital voltmeter.
12
Read the voltmeter to 3 figures but assign uncertainty based on the apparent reproducibility of readings.
13
Test Cu with each of different metals provided.
14
Compare your calculated theoretical E° values with your measured values. Find the percent error to three significant figures.
Part 2: Dependence of E on Ion Concentrations
In part 1 you measured E° values. In part 2, you will read about how E depends on concentration of ions in a concentration cell. In a concentration cell, both electrodes are made of the same metal and the solutions in the cells are of the same ion as the electrodes. The difference between the cells lies in the metal ion concentration. In this case, the chemical reaction is given below.( 16 )
Ag(s) + Ag+(conc)  Ag(s) + Ag+(dil)
Ag(s) + Ag+(dil)
 Ag(s) + Ag+(dil)
Ag(s) + Ag+(dil) ( 17 )
E = −
log10
| (0.0591 volts) |
| n |
| Ag+dil |
| Ag+conc |
-
•In cell 1, ions accept electrons from the metal, plate out on the electrode, and lower the concentration of the ions.
-
•In cell 2, atoms in the metal leave electrons behind and enter the solution, thus raising the ion concentration.
-
•The reaction occurs in such a direction as to equalize the concentrations of the two solutions.
Ksp
determinations in part 3.
1
Your data table from this part should have columns for E, c2, and c1.
2
Label six vials as follows: two of 10–1 M, and one each of 10–2, 10–3, 10–4, and 10–5 M. There are Ag+ solutions with which to fill these vials, 2/3 full as before.
3
Use two Ag wire electrodes.
4
Set up concentration cells in which c1 is 10–1 M.
5
Use all five of the other solutions for c2.
6
Measure each voltage and polarity.
7
Measure the temperature of the lab to determine if this might cause error due to temperature difference from 25°C (assumed in calculation of slope). Also, the temperature is needed in part 3 for the calculation of ΔG of solubility from Ksp.
8
Add another column in your data table for log (c2/c1).
9
In accordance with Eq. 17E = −
log10
, prepare a plot of voltage E against log (c2/c1).
| (0.0591 volts) |
| n |
| Ag+dil |
| Ag+conc |
10
Fit the best straight line to your data points. Determine the slope of the best fit line.
11
Compare your experimental slope with that given in Eq. 17E = −
log10
(–0.0591 V/n).
| (0.0591 volts) |
| n |
| Ag+dil |
| Ag+conc |
12
The concentration dependence of the voltage (the slope) is used in part 3 to determine the Ag+ concentration in saturated AgX(s) solutions. And, part 2 can be considered a calibration for part 3 because the experimental Nernst slope found in part 2 may be used in determining Ksp values.
NOTE:
Depending on the lab schedule, part 2 might be omitted. Your TA will inform you in lab. If part 2 is not performed, use the plot that would be obtained ideally (theoretical) from plotting E vs. log([Ag+dil]/[Ag+conc]).( 18 )
| E | = | −
| ||||
| y | = | m · x |
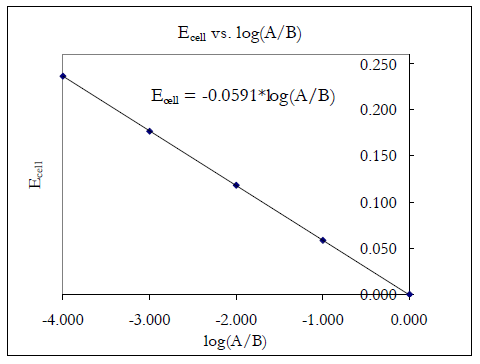
Figure 2
Part 3: Determination of Ksp of Very Insoluble Silver Halides
In this step you will determine the concentration of Ag+ ion in a saturated solution of silver halides (AgCl, AgBr, and AgI) by measuring the voltage of a concentration cell in which the silver halide solution is paired with 0.10 M Ag+. There are 0.20 M stock solutions of KCl, KBr, and KI. To measure Ksp for AgCl:1
Put KCl solution into one of your vials and 0.10 M Ag+ in the other.
2
To the vial containing KCl add 1 drop of 0.10 M AgNO3. You should observe the formation of a small amount of the white precipitate AgCl. If you don't, add another drop. The fact that solid AgCl precipitated in your vial means that AgCl(s) is in equilibrium with Ag+ and Cl– ions, so the solubility product condition is satisfied in your vial: Ksp = [Ag+][Cl–].
3
Clamp the vials together and insert the salt bridge.
4
Since this is a concentration cell, use silver electrodes in both vials.
5
Measure the voltage and polarity of this cell.
6
Do the same experiment with KBr to study the solubility of AgBr.
7
Use KI to study the solubility of AgI.
8
You have obtained enough information to determine the value of Ksp. The same applies to [Br–] or [I–] for AgBr or AgI.
Ksp for the three silver halides are [Ag+]dil[Cl–] or [Ag+]dil[Br–] or [Ag+]dil[I–].
The concentration of the halide ion is ~0.20 M, its initial molarity. Very little Ag+ ion was added, so very little Cl– reacted to form AgCl. Thus, the value of [Cl–] is essentially unchanged from its initial.
[Ag+]dil is determined from the cell voltage and from Eq. 17
E = −
log10
: [Ag+]conc is assumed to be 0.10 M (relatively unchanged from its initial value). E is the measured cell potiention in volts.
| (0.0591 volts) |
| n |
| Ag+dil |
| Ag+conc |
9
Calculate all three values of Ksp to two significant figures.
10
Compare the experimental values of Ksp with the literature values.
Literature value of Ksp for AgBr = 5.3 e-13
Literature value of Ksp for AgCl = 1.8 e-10
Literature value of Ksp for AgI = 8.3 e-17
11
Calculate ΔG° for the reaction, AgX  Ag+ + X–, using ΔG° = –RT ln Ksp, to three significant figures.
Do not use
Ag+ + X–, using ΔG° = –RT ln Ksp, to three significant figures.
Do not use ΔG° = −nFEmeasured
Results
Complete your lab summary or write a report (as instructed).Abstract
Results
-
Part 1. Data and Results table
- Emeasured for various metals relative to Cu (i.e. Cu__M1),
- E°(cell) predicted using metals other than copper
-
Part 2. Data and Results Table if done
- c1(0.10 M), c2, Emeasured, and log(c2/c1)
- graph E versus log (c2/c1), and determine the slope
-
Part 3. Data and Results
- Emeasured, cAg+, Ksp for AgCl, AgBr, AgI, and ΔG°
Sample Calculations
- Part 1. Predicted E° for cells with metals vs. Cu
- Part 2. log(c2/c1) if done
- Part 3. [Ag+], Ksp(AgCl), ΔG°(AgCl solubility), Ksp(AgBr), ΔG°(AgBr solubility), Ksp(AgI), ΔG°(AgI solubility)
Discussion/Conclusions
- Part 1: Does Emeasured agree with Epredicted for the various metals?
- Part 2: Does the slope agree with the slope predicted by the Nernst equation?
-
Part 1 and 2:
- Even though cell potentials are affected by both concentration differences and voltage differences between different metals, you were able to determine the dependence on each factor (RT / nF and E1/2°). How were the individual dependencies separated out and determined individually?
- Part 3: How does part 3 depend on part 2?
