Lab 8 - Acids, Bases, Salts, and Buffers
Goal and Overview
Hydrolysis of salts will be used to study the acid-base properties of dissolved ions in aqueous solutions. The approximate pH of these solutions will be determined using acid-base indicators. A buffer solution will be prepared, and its ability to moderate pH will be investigated alongside solutions that cannot function as buffers.Objectives and Science Skills
-
•Analyze the colors of different pH indicators to estimate the pH of deionized water and of aqueous solutions containing soluble ionic compounds.
-
•Calculate the approximate Ka or Kb of an ion in solution based on a pH estimate and compare to expected values.
-
•Perform volumetric dilutions and calculate resulting molarities.
-
•Qualitatively and quantitatively analyze and explain the effect of adding strong base to a weak acid, a weak base, and a buffer; explain how a buffer resists changes in pH upon the addition of small amounts of strong base (or acid).
-
•Identify and discuss factors or effects that may contribute to deviations between theoretical and experimental results and formulate optimization strategies.
Suggested Review and External Reading
-
•data analysis review; relevant textbook information on acids, bases, salts, and buffers
Background
Weak acids and bases in water
Brønsted-Lowry acids are proton donors and bases are proton acceptors. In water, an acid can donate a proton to water to form aqueous H+ and the conjugate base; a base can accept a proton from water to form OH– and the conjugate acid. In acidic solutions, the concentration of H+(aq) is greater than the OH– concentration and the pH is less than 7, while the reverse is true in basic solutions ([H+] < [OH– ], pH > 7). Aqueous solutions of substances such as HCl or HC2H3O2 are expected to be acidic, while aqueous solutions of substances such as NaOH or NH3 are expected to be basic. The dissolution of some salts into water can affect pH. For example, aqueous solutions of NaNO2 and KC2H3O2 are basic, whereas those of NH4Cl and FeCl3 are acidic. The dissolved ions have the potential to undergo proton transfer reactions with water to generate H+ or OH–. Anions that are the conjugate bases of weak acids react with water to form OH–(aq). Cations that are the conjugate acids of weak bases can undergo a proton transfer reaction with water to generate H+(aq). Let HA represent a weak acid and A– its conjugate base. A weak acid is one which does not completely dissociate in or react with a water solution. Instead, equilibrium is established. The equilibrium constant is called the acid dissociation constant, Ka.( 1 )
HA(aq)  A–(aq) + H+(aq)
A–(aq) + H+(aq)
 A–(aq) + H+(aq)
A–(aq) + H+(aq)( 2 )
Ka =
| [H+][A− ] |
| [HA] |
( 3 )
A–(aq) + H2O(l)  HA(aq) + OH–(aq)
HA(aq) + OH–(aq)
 HA(aq) + OH–(aq)
HA(aq) + OH–(aq)( 4 )
Kb =
| [OH− ][HA] |
| [A− ] |
( 5 )
| HA(aq) |  | A−(aq) + H+(aq) |
| A−(aq) + H2O(l) |  | HA(aq) + OH−(aq) |
( 6 )
H2O(l)  H+(aq) + OH–(l)
H+(aq) + OH–(l) ( 7 )
KaKb =
×
= [H+][OH− ] = Kw.
| [H+][A− ] |
| [HA] |
| [HA][OH− ] |
| [A− ] |
NO2−(aq) + H2O(l)  HNO2(aq) + OH−(aq) HNO2(aq) + OH−(aq) | Ka of HNO2 = 4.5 × 10−4 | |||||
| Kb for NO2− is: | Kb =
|
NH4+(aq)  NH3(aq) + H+(aq) NH3(aq) + H+(aq) | Kb of NH3 = 1.8 × 10–5 | |||||
| Ka for NH4+ is: | Ka =
|
Example: Fe(H2O)63+(aq)  Fe(H2O)5(OH)2+(aq) + H+(aq) Ka of Fe3+(aq) = 1.5 x 10–3
Fe(H2O)5(OH)2+(aq) + H+(aq) Ka of Fe3+(aq) = 1.5 x 10–3
Anions with ionizable protons such as HCO3–, H2PO4–, and HPO42– are amphoteric – they may be acidic or basic, depending on the values of Ka and Kb for the ion. These types of species will not be considered in this lab.
 Fe(H2O)5(OH)2+(aq) + H+(aq) Ka of Fe3+(aq) = 1.5 x 10–3
Fe(H2O)5(OH)2+(aq) + H+(aq) Ka of Fe3+(aq) = 1.5 x 10–3
The acidity, basicity, or neutrality of an aqueous salt solution can be predicted based on the strengths of the acid and base from which the salt was derived.
-
1Cation from strong base; anion from strong acid
- Ex. NaCl, KNO3
- Solution has pH = 7 (neutral)
-
2Cation from weak base; anion from strong acid
- Ex. NH4Cl, Zn(NO3)2
- Solution has pH < 7 (acidic) due to the hydrolysis of the cation
-
3Cation from strong base; anion from weak acid
- Ex. NaF, KNO2
- Solution has pH > 7 (basic) due to the hydrolysis of the anion
-
4Cation from weak base; anion from weak acid
- Ex. NH4F, NH4C2H3O2
- Solution pH is determined by the relative Ka and Kb of the cation and anion
Buffers
A buffer solution resists large changes in pH upon the addition of small amounts of strong acid or strong base. A buffer has two components: one that will react with added H+ and one that will react with added OH–. Usually these two parts are a weak acid and its conjugate base (or vice versa). Buffers are often prepared by mixing a weak acid (or weak base) with a salt of that acid (or base). For example, a buffer could be made by adding NaC2H3O2 solution to an HC2H3O2 solution. Buffers of almost any pH can be made by proper choice of components and concentrations. If significant concentrations of both a weak acid, HA, and its conjugate base, A–, are present in the solution:-
•
added OH– reacts with the weak acid: HA + OH–  H2O + A–
H2O + A–K1 = 1/Kb, A– -
•
added H+ reacts with the conjugate base: A– + H+  HA
HAK2 = 1/Ka, HA.
( 8 )
HA  H+ + A– [H+] = Ka ×
H+ + A– [H+] = Ka ×
 H+ + A– [H+] = Ka ×
H+ + A– [H+] = Ka × | [HA] |
| [A– ] |
-
•the value of Ka for the acid component of the buffer; and,
-
•the ratio of the weak acid to its conjugate base ([HA]/[A– ]).
Ka = [H+]
= [H+] × 1 = [H+] or pH = pKa.
The Henderson-Hasselbach equation is often used to calculate approximate buffer pH.
| [A– ] |
| [HA] |
( 9 )
pH = pKa + log
| [A− ] |
| [HA] |
KaKb =
×
= [H+][OH− ] = Kw.
| [H+][A− ] |
| [HA] |
| [HA][OH− ] |
| [A− ] |
Procedure
Caution:
You are working with acids and bases. Handle them with caution and clean up spills.
You are working with acids and bases. Handle them with caution and clean up spills.
Part 1: Salts and Solution pH (proton transfer reactions in water)
1
Boil approximately 250 mL deionized water and allow it to cool to room temperature. Use caution when heating/handling.
2
Determine the approximate pH of two water samples and six 0.1 M salt solutions by observing each solution's color in the presence of six different indicators.
The eight liquid samples to test are:
-
•unboiled deionized water
-
•boiled deionized water
-
•0.1 M NaCl
-
•0.1 M NH4Cl
-
•0.1 M NaC2H3O2
-
•0.1 M ZnCl2
-
•0.1 M KAl(SO4)2
-
•0.1 M Na2CO3
-
•methyl orange
-
•methyl red
-
•bromothymol blue
-
•phenol red
-
•phenolphthalein
-
•alizarin yellow-R
3
Use the schematics below as a guide. Rinse the well plate with a small amount of boiled deionized water and dry it before and after each set of observations.
Figure 1: Set 1
Figure 2: Set 2
4
Place 1 drop of an indicator into a well. Add a small volume (about 1 'squirt' from the pipet) of the solution to be tested. Do not completely fill each well (about 1/2 way is enough). Test the solutions in two batches, four at a time.
5
Record the color in each well for each solution.
6
Wash the well plate thoroughly when finished and return it to the reagent bench.
7
Estimate the pH of each solution based on the indicator colors. Each solution has one pH value, not multiple pH values. So, for eight solutions, you should have eight pH values (one for each). Report each pH value to the tenths place.
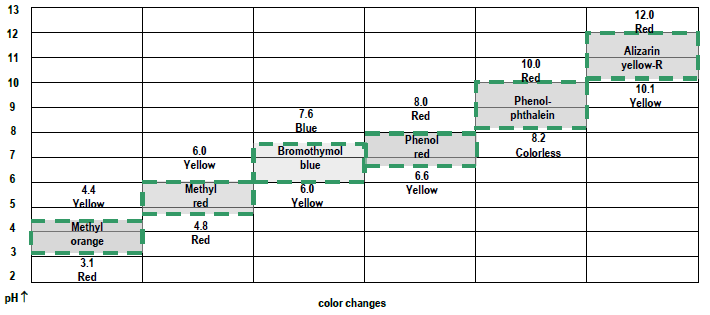
Figure 3: Indicator colors as a function of pH:
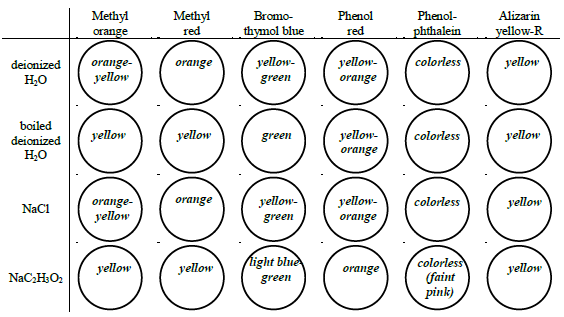
Figure 4: Example pH values based on colors:
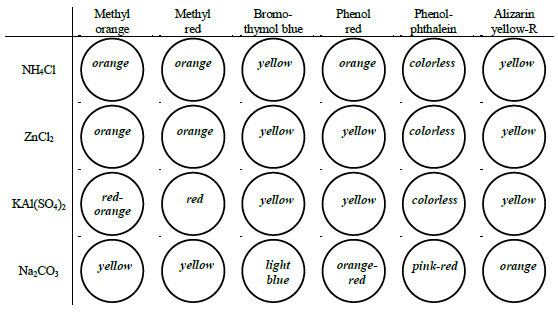
Figure 5: Example pH values based on colors:
How to estimate the pH of — Na2CO3 as an example:
- methyl orange appears yellow – pH is above 4.4
- methyl red appears yellow – pH is above 6.0
- bromothymol blue appears blue – pH is above 7.6
- phenol red appears red – pH is above 8.0
- phenolphthalein appears pink – pH is above 10.0
- alizarin yellow-R appears orange – pH is in this range (~10.4)
- methyl orange appears orange – pH is in this range (~3.8)
- methyl red appears red – pH is below 4.8
- no further data needed, but:
- bromothymol blue appears yellow – pH is below 6.0
- phenol red appears yellow – pH is below 6.6
- phenolphthalein appears pink – pH is below 8.2
- alizarin yellow-R appears orange – pH is below 10.1
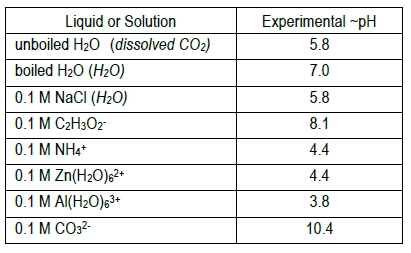
8
The equilibrium expression(s) for the expected proton transfer reaction(s) in each solution are given below. Do your estimated pH values reflect the presence of excess H+ or OH– predicted by the reactions?
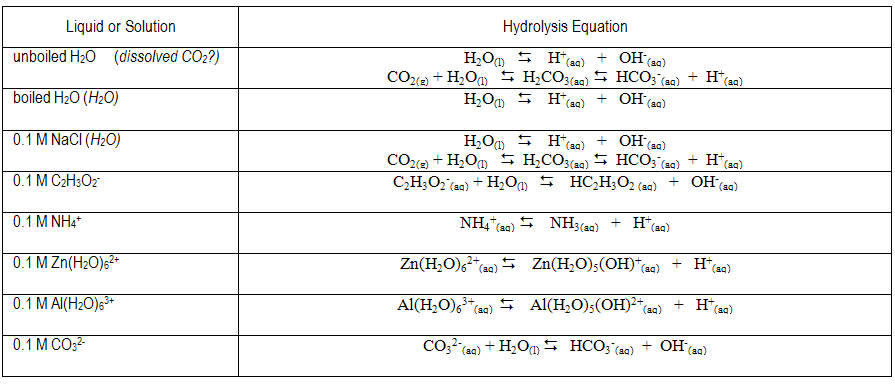
9
Using your pH values and the concentration of the solution, calculate the Ka or Kb for each cation or anion that hydrolyzes to two significant figures. Compare your calculated value to the literature value and give possible explanations for the deviation (if any).
Literature values:
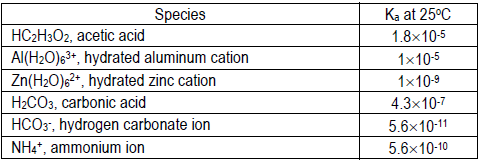

If you need a Kb value, recall Kb = Kw/Ka
Recall:
-
HA(aq)  A–(aq) + H+(aq)
A–(aq) + H+(aq)and Ka = [H+][A– ] [HA] A–(aq) + H2O(l)  HA(aq) + OH–(aq)
HA(aq) + OH–(aq)and Kb =
.[OH– ][HA] [A– ]
Please assume the percent dissociation is small relative to the initial concentration of acid or base (0.1 M). In the weak acid solutions, recall [H+] = 10–pH, and please assume [H+] ≈ [A– ] at equilibrium. In the weak base solutions, recall [OH– ] = 1 × 10–14/[H+], and please assume [OH–] ≈ [HA] at equilibrium.
Example calculations:
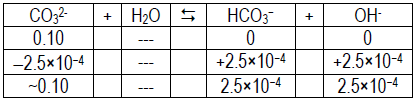

- Using pH = 10.4 for CO32– solution: pOH = 14 – 10.4 = 3.6, so [OH– ] = 2.5 × 10–4.
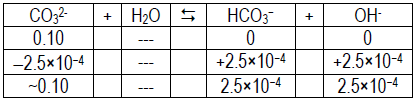
-
Kb =
≈[OH– ][HA] [A– ]
= 6.3 × 10–7[2.5 × 10–4]2 [0.10]

-
Ka =
≈[H+][A– ] [HA]
= 2.6 × 10–7[1.6 × 10–4]2 [0.10]
The percent error relative to the literature values may be quite large. Think about how you determined the pH and how precise those values were. Also consider the impact of the log relationship between pH and [H+], as well as the assumptions you made.
Part 2a: pH of Buffer Solutions
1
Obtain about 10 mL 1 M acetic acid (HC2H3O2, "HAc") and about 10 mL 1 M sodium acetate (NaC2H3O2, "NaAc") solutions in small, labeled beakers.
2
Pipet 5 mL 1 M HAc into a labeled 100 mL volumetric flask and dilute to the mark with water.
3
Pipet 5 mL 1 M NaAc into a labeled 100 mL volumetric flask and dilute to the mark with water.
4
Pipet 5 mL 1 M HAc into a labeled 100 mL volumetric flask; pipet into the same flask 5 mL 1 M NaAc(aq). Dilute to the mark with water.
5
The above steps should provide you with 100 mL of each of the following: acetic acid solution (HAc), acetate (NaAc) solution, and acetic acid/acetate solution (HAc/Ac–). Calculate the initial molarity of HAc, Ac–, and HAc, Ac– in each solution.
6
Measure the pH of the solutions using a calibrated pH meter (see instructions in lab). The pH meters are delicate and you need to read the printed instructions carefully (and follow the TA's instructions, too). Record each pH value to two decimal places.
7
Save the solutions for part 2b.
8
Calculate the expected pH of the 0.05 M HAc, 0.05 M Ac–, and 0.05 M HAc/0.05 M Ac–. Your pH values should be ~3.02, 8.72, and 4.74, respectively. Compare your measured value to the theoretical value and give possible explanations for the deviation (if any).
ICE table to help you get started:

Part 2b: Effect of Acid and Base on Buffer pH
9
Pipet 1 mL 1.0 M NaOH into the HAc solution and record the pH.
Note – there is a weak acid present to react with the added OH–. Do you expect a huge jump in pH here?
10
Pipet 1 mL 1.0 M NaOH into the Ac– solution and record the pH.
Note – there is only a weak base present in the initial solution, so what do you think added OH– will do to the pH here?
11
Pipet 1 mL 1.0 M NaOH into the HAc/Ac– and record the pH.
Note – the original solution is a buffer, so do you expect the pH change to be relatively large or small here?
12
Please clean the pH meter and leave the electrode immersed in the pH = 7 buffer (yellow solution).
| Waste disposal: | Follow your TA's instructions. | |
| Clean all equipment and return it to the correct location. |
13
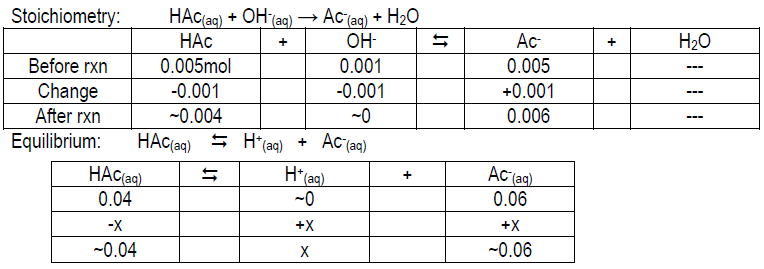
Calculate the expected pH of 0.05 M HAc, 0.05 M Ac–, and 0.05 M HAc/0.05 M Ac– after the addition of 1 mL 1.0 M NaOH to each. Your values should be ~4.14, 12.00, and 4.92, respectively. Compare your measured pH value to the theoretical value and give possible explanations for the deviation (if any).
Tables to help you get started:
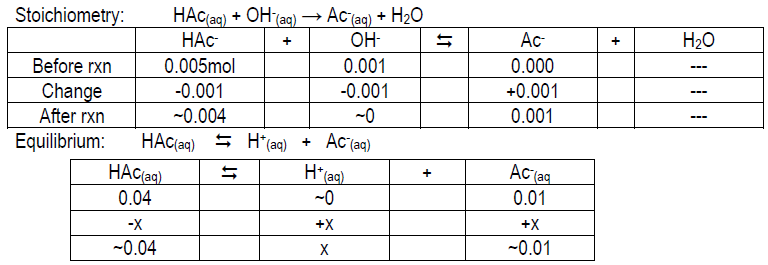
Stoichiometry: Ac–(aq) + OH–(aq) → Ac–(aq) + OH–(aq); think about [OH– ] from NaOH vs. Ac–
Reporting Results
Complete your lab summary or write a report (as instructed).Abstract
Results
Part 1. Hydrolysis equation for each solution; Ka or Kb of each liquid or solution; percent error
Part 2a. Measured and expected pH of solutions before OH– addition
Part 2b. Measured and expected pH of solutions after OH– addition
Sample Calculations
Part 1. Ka or Kb of each hydrolyzed species; percent error
Part 2a. Expected pH of solutions before OH– addition
Part 2b. Expected pH of solutions after OH– addition
Discussion/Conclusions
Part 1. Did the pH of the solutions match what might be predicted based on the cation and anion provided by the salt? How good were your measured Ka or Kb values?
Part 2a. Did the measured pH match the expected pH?
Part 2b. Did the measured pH match the expected pH? Which solution showed the greatest change in pH? Which showed the least? Why?
