X
Explore It
Close

YOU WILL LEARN ABOUT:

The Mean Value Theorem for Derivatives.

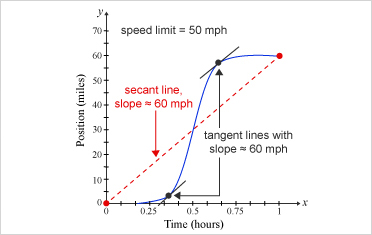
t27_concept_01 t27_concept_02

In the diagram above, imagine an officer noting the time in which an individual enters and exits a toll road (via the time stamps on the receipts or stubs). The officer could issue a ticket based on the Mean Value Theorem if the ratio of the distance traveled (f(b)-f(a)) to the travel time (b−a) is greater than the speed limit. The MVT states that at some point between a and b, the slope of the graph (the speed of the car at an instant) must be equal to the slope of the secant line through the endpoints. In other words, there must be some c in the interval (a,b) such that f'(c)=f(b) - f(a)b - a.

Many real-world situations are described by functions that are continuous and differentiable. Characteristics of the functions, and therefore the situations themselves, can be understood using the Mean Value Theorem for Derivatives.

t27_when_img_01
If a person is emptying a septic tank, the original volume of sewage divided by the time it takes to empty the tank gives the average flow rate. There must be a moment when the liquid is draining at precisely that average flow rate.
t27_when_img_02
Many environmentalists study human activities that can lead to global warming. If the temperature of a location is measured consistently over a period of time, the temperature’s average rate of change over the entire period must have been the actual rate of change at some point during the period.
t27_when_img_03
Mechanical engineers often study how objects behave as they fall. When an object falls from a height, the time it takes to fall that distance determines its average velocity. There must be a moment during its fall when the object’s velocity was exactly that average velocity.

Mean Value Theorem for Derivatives
Click Show to view all the necessary information about the function, parameters, and slopes.

close
Show secant line
Show movable tangent line
Show tangent line at points that satisfy the Mean Value Theorem
f(x)
=a0+a1x+a2x2+a3x3
=0.00−2.00x+1.00 x 2+1.00 x 3
a 0=0.00
a 1=−2.00
a 2=1.00
a 3=1.00
P=−0.75

slope of secant: 7.00

slope of tangent at P:− 1.81

c 1=−2.10
c 2=1.43
Show secant line
Show movable tangent line
Show tangent lines at points that satisfy the Mean Value Theorem
g ( x )
= a 1 sin ( a 2 x )
= 3.00 sin ( 2.00 x )
a 1 = 3.00
a 2 = 2.00
P = 2.62

slope of secant: 0.00

slope of tangent at P: 3.00

c 1=0.79
c 2=2.36
c 3=3.93
c 4=1.43
c 5=3.93
c 6=1.43
Show secant line
Show movable tangent line
Show tangent lines at points that satisfy the Mean Value Theorem
h(x)
= a 1 e a 2x+ a 3
= 2.00e 0.50x − 3.00
a 1=2.00
a 2=0.50
a 3=−3.00
P=2.25

slope of secant : 1.42

slope of tangent at P:3.08

c=0.70

Equation of the line tangent to the graph of (x)  : y = (x − )

INSTRUCTIONS

Change the values of the parameters to see how the graph changes. Notice that there is always at least one point between a and b where the slope of the tangent line is equal to the slope of the secant line between (a,f(a)) and (b,f(b)).
(Click the Show button below the graph to view necessary information about the function, parameters, and slopes. From within the information box, you can manipulate the parameters and graph features. Note that the box can be dragged as necessary to better view the graph.)

PRACTICE QUESTIONS

1 2 3
1. For the function f(x)=1+2.5x−2x2−x3, find all values of c that satisfy the conclusion of the Mean Value Theorem on the interval [−1,2]. Be sure to select each such value of c.
2. For the function f(x)=1.5−2x−3 x2+x3, find all values of c that satisfy the conclusion of the Mean Value Theorem on the interval [−1,2]. Select the correct value or values below.
3. How many values of c satisfy the conclusion of the Mean Value Theorem for a cubic function on a closed interval?

INSTRUCTIONS

Change the values of the parameters to see how the graph changes. Notice that there is always at least one point between a and b where the slope of the tangent line is equal to the slope of the secant line between
(a,g(a)) and (b,g(b)).
(Click the Show button below the graph to view necessary information about the function, parameters, and slopes. From within the information box, you can manipulate the parameters and graph features. Note that the box can be dragged as necessary to better view the graph.)

PRACTICE QUESTIONS

1 2 3
1. For the function g(x) =−2.5sin(2x), how many values of c are there that satisfy the conclusion of the Mean Value Theorem on the interval [0,2π]?
2. For the function g(x) =2cos(3x), find all values of c that satisfy the conclusion of the Mean Value Theorem on the interval [ π2,3π2]. Be sure to select each such value of c.
3. Consider the function g(x) =2sin(1.5x), on the interval [ π6,b]. If there are exactly three values of c that satisfy the conclusion of the Mean Value Theorem, what could be the value of b? Select all that apply.

INSTRUCTIONS

Change the values of the parameters to see how the graph changes. Notice that there is always at least one point between a and b where the slope of the tangent line is equal to the slope of the secant line between (a,h(a)) and (b,h(b)).
(Click the Show button below the graph to view necessary information about the function, parameters, and slopes. From within the information box, you can manipulate the parameters and graph features. Note that the box can be dragged as necessary to better view the graph.)

PRACTICE QUESTIONS

1 2 3
1. For the function h(x)=ex, find all values of c that satisfy the conclusion of the Mean Value Theorem on the interval [−2,1]. Be sure to select each such value of c.
2. For the function h(x)= −0.25e0.5x+2, find all values of c that satisfy the conclusion of the Mean Value Theorem on the interval [−1,3]. Be sure to select each such value of c.
3. How many values of c can satisfy the conclusion of the Mean Value Theorem for an exponential function on a closed interval?
Result