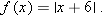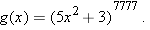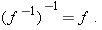| 1.5 | Inverse Functions |
|
|||||||||||||||||||||||
The Inverse Problem
The concept of an inverse function will play a key role in this book in defining roots, logarithms, and inverse trigonometric
functions. To motivate this concept, we begin with some simple examples.
Suppose  is the function defined by
is the function defined by 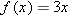 . Given a value of
. Given a value of  , we can find the value of
, we can find the value of 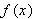 by using the formula defining
by using the formula defining  . For example, taking
. For example, taking 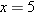 , we see that
, we see that 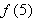 equals
equals 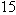 .
.
 is the function defined by
is the function defined by 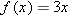 . Given a value of
. Given a value of  , we can find the value of
, we can find the value of 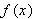 by using the formula defining
by using the formula defining  . For example, taking
. For example, taking 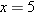 , we see that
, we see that 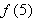 equals
equals 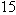 .
.
In the inverse problem, we are given the value of 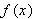 and asked to find the value of
and asked to find the value of  . The following example illustrates the idea of the inverse problem:
. The following example illustrates the idea of the inverse problem:
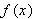 and asked to find the value of
and asked to find the value of  . The following example illustrates the idea of the inverse problem:
. The following example illustrates the idea of the inverse problem:
|
||||||||||||||||||||||||||||
For each number  , part (c) of the example above asks for the number
, part (c) of the example above asks for the number  such that
such that 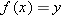 . That number
. That number  is called
is called 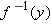 (pronounced “
(pronounced “ inverse of
inverse of  ”). The example above shows that if
”). The example above shows that if 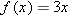 , then
, then 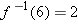 and
and 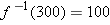 and, more generally,
and, more generally, 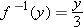 for every number
for every number  .
.
 , part (c) of the example above asks for the number
, part (c) of the example above asks for the number  such that
such that 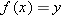 . That number
. That number  is called
is called 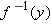 (pronounced “
(pronounced “ inverse of
inverse of  ”). The example above shows that if
”). The example above shows that if 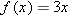 , then
, then 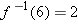 and
and 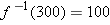 and, more generally,
and, more generally, 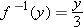 for every number
for every number  .
.
|
To see how inverse functions can arise in real-world problems, suppose you know that a temperature of  degrees Celsius corresponds to
degrees Celsius corresponds to 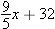 degrees Fahrenheit (we will derive this formula in Example 5 in Section 2.1). In other words, you know that the function
degrees Fahrenheit (we will derive this formula in Example 5 in Section 2.1). In other words, you know that the function
 that converts the Celsius temperature scale to the Fahrenheit temperature scale is given by the formula
that converts the Celsius temperature scale to the Fahrenheit temperature scale is given by the formula
 degrees Celsius corresponds to
degrees Celsius corresponds to 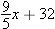 degrees Fahrenheit (we will derive this formula in Example 5 in Section 2.1). In other words, you know that the function
degrees Fahrenheit (we will derive this formula in Example 5 in Section 2.1). In other words, you know that the function
 that converts the Celsius temperature scale to the Fahrenheit temperature scale is given by the formula
that converts the Celsius temperature scale to the Fahrenheit temperature scale is given by the formula
|
|
If you are given a temperature on the Fahrenheit scale and asked to convert it to Celsius, then you are facing the problem
of finding the inverse of the function above, as shown in the following example.
|
||||||||||||||||||||||||||||||||
In the example above we have 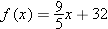 . For each number
. For each number  , part (b) of the example above asks for the number
, part (b) of the example above asks for the number  such that
such that 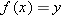 . We call that number
. We call that number 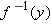 . Part (a) of the example above shows that
. Part (a) of the example above shows that 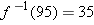 ; part (b) shows more generally that
; part (b) shows more generally that
In this example, the function  converts from Celsius to Fahrenheit, and the function
converts from Celsius to Fahrenheit, and the function  goes in the other direction, converting from Fahrenheit to Celsius.
goes in the other direction, converting from Fahrenheit to Celsius.
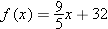 . For each number
. For each number  , part (b) of the example above asks for the number
, part (b) of the example above asks for the number  such that
such that 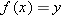 . We call that number
. We call that number 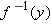 . Part (a) of the example above shows that
. Part (a) of the example above shows that 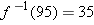 ; part (b) shows more generally that
; part (b) shows more generally that
|
 converts from Celsius to Fahrenheit, and the function
converts from Celsius to Fahrenheit, and the function  goes in the other direction, converting from Fahrenheit to Celsius.
goes in the other direction, converting from Fahrenheit to Celsius.
One-to-one Functions
To see the difficulties that can arise with inverse problems, consider the function  , with domain the set of real numbers, defined by the formula
, with domain the set of real numbers, defined by the formula
Suppose we are told that  is a number such that
is a number such that 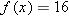 , and we are asked to find the value of
, and we are asked to find the value of  . Of course
. Of course 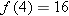 , but also
, but also 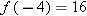 . Thus with the information given we have no way to determine a unique value of
. Thus with the information given we have no way to determine a unique value of  such that
such that 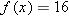 . Hence in this case an inverse function does not exist.
. Hence in this case an inverse function does not exist.
 , with domain the set of real numbers, defined by the formula
, with domain the set of real numbers, defined by the formula
|
 is a number such that
is a number such that 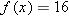 , and we are asked to find the value of
, and we are asked to find the value of  . Of course
. Of course 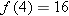 , but also
, but also 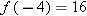 . Thus with the information given we have no way to determine a unique value of
. Thus with the information given we have no way to determine a unique value of  such that
such that 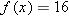 . Hence in this case an inverse function does not exist.
. Hence in this case an inverse function does not exist.
The difficulty with the lack of a unique solution to an inverse problem can often be fixed by changing the domain. For example,
consider the function  , with domain the set of positive numbers, defined by the formula
, with domain the set of positive numbers, defined by the formula
Note that  is defined by the same formula as
is defined by the same formula as  in the previous paragraph, but these two functions are not the same because they have different domains. Now if we are told
that
in the previous paragraph, but these two functions are not the same because they have different domains. Now if we are told
that  is a number in the domain of
is a number in the domain of  such that
such that 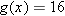 and we are asked to find
and we are asked to find  , we can assert that
, we can assert that 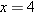 . More generally, given any positive number
. More generally, given any positive number  , we can ask for the number
, we can ask for the number  in the domain of
in the domain of 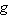 such that
such that 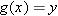 . This number
. This number  , which depends on
, which depends on  , is denoted
, is denoted 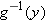 , and is given by the formula
, and is given by the formula
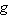 , with domain the set of positive numbers, defined by the formula
, with domain the set of positive numbers, defined by the formula
|
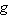 is defined by the same formula as
is defined by the same formula as  in the previous paragraph, but these two functions are not the same because they have different domains. Now if we are told
that
in the previous paragraph, but these two functions are not the same because they have different domains. Now if we are told
that  is a number in the domain of
is a number in the domain of 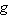 such that
such that 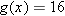 and we are asked to find
and we are asked to find  , we can assert that
, we can assert that 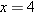 . More generally, given any positive number
. More generally, given any positive number  , we can ask for the number
, we can ask for the number  in the domain of
in the domain of 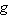 such that
such that 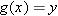 . This number
. This number  , which depends on
, which depends on  , is denoted
, is denoted 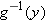 , and is given by the formula
, and is given by the formula
|
We saw earlier that the function  defined by
defined by 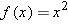 (and with domain equal to the set of real numbers) does not have an inverse because, in particular, the equation
(and with domain equal to the set of real numbers) does not have an inverse because, in particular, the equation 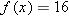 has more than one solution. A function is called one-to-one if this situation does not arise.
has more than one solution. A function is called one-to-one if this situation does not arise.
 defined by
defined by 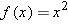 (and with domain equal to the set of real numbers) does not have an inverse because, in particular, the equation
(and with domain equal to the set of real numbers) does not have an inverse because, in particular, the equation 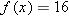 has more than one solution. A function is called one-to-one if this situation does not arise.
has more than one solution. A function is called one-to-one if this situation does not arise.
|
For example, the function  , with domain the set of real numbers, defined by
, with domain the set of real numbers, defined by 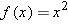 is not one-to-one because there are two distinct numbers
is not one-to-one because there are two distinct numbers  in the domain of
in the domain of  such that
such that 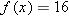 (we could have used any positive number instead of
(we could have used any positive number instead of 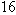 to show that
to show that  is not one-to-one). In contrast, the function
is not one-to-one). In contrast, the function 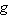 , with domain the set of positive numbers, defined by
, with domain the set of positive numbers, defined by 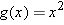 is one-to-one.
is one-to-one.
 , with domain the set of real numbers, defined by
, with domain the set of real numbers, defined by 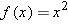 is not one-to-one because there are two distinct numbers
is not one-to-one because there are two distinct numbers  in the domain of
in the domain of  such that
such that 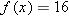 (we could have used any positive number instead of
(we could have used any positive number instead of 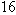 to show that
to show that  is not one-to-one). In contrast, the function
is not one-to-one). In contrast, the function 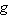 , with domain the set of positive numbers, defined by
, with domain the set of positive numbers, defined by 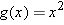 is one-to-one.
is one-to-one.
The Definition of an Inverse Function
We are now ready to give the formal definition of an inverse function.
|
||||||||||||||||||||
|
||||||||||||||||||||||||
If  is a one-to-one function, then for each
is a one-to-one function, then for each  in the range of
in the range of  we have a uniquely defined number
we have a uniquely defined number 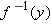 . Thus
. Thus  is itself a function.
is itself a function.
 is a one-to-one function, then for each
is a one-to-one function, then for each  in the range of
in the range of  we have a uniquely defined number
we have a uniquely defined number 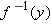 . Thus
. Thus  is itself a function.
is itself a function.
|
Think of  as undoing whatever
as undoing whatever  does. This list gives some examples of a function
does. This list gives some examples of a function  and its inverse
and its inverse  .
.
 as undoing whatever
as undoing whatever  does. This list gives some examples of a function
does. This list gives some examples of a function  and its inverse
and its inverse  .
.
|
The first entry in the list above shows that if  is the function that adds
is the function that adds 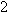 to a number, then
to a number, then  is the function that subtracts
is the function that subtracts 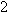 from a number.
from a number.
 is the function that adds
is the function that adds 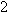 to a number, then
to a number, then  is the function that subtracts
is the function that subtracts 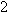 from a number.
from a number.
The second entry in the list above shows that if  is the function that multiplies a number by
is the function that multiplies a number by 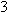 , then
, then  is the function that divides a number by
is the function that divides a number by 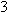 .
.
 is the function that multiplies a number by
is the function that multiplies a number by 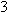 , then
, then  is the function that divides a number by
is the function that divides a number by 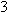 .
.
Similarly, the third entry in the list above shows that if  is the function that squares a number, then
is the function that squares a number, then  is the function that takes the square root of a number (here the domain of
is the function that takes the square root of a number (here the domain of  is assumed to be the nonnegative numbers, so that we have a one-to-one function).
is assumed to be the nonnegative numbers, so that we have a one-to-one function).
 is the function that squares a number, then
is the function that squares a number, then  is the function that takes the square root of a number (here the domain of
is the function that takes the square root of a number (here the domain of  is assumed to be the nonnegative numbers, so that we have a one-to-one function).
is assumed to be the nonnegative numbers, so that we have a one-to-one function).
Finally, the fourth entry in the list above shows that if  is the function that takes the square root of a number, then
is the function that takes the square root of a number, then  is the function that squares a number (here the domain of
is the function that squares a number (here the domain of  is assumed to be the nonnegative numbers, because the square root of a negative number is not defined as a real number).
is assumed to be the nonnegative numbers, because the square root of a negative number is not defined as a real number).
 is the function that takes the square root of a number, then
is the function that takes the square root of a number, then  is the function that squares a number (here the domain of
is the function that squares a number (here the domain of  is assumed to be the nonnegative numbers, because the square root of a negative number is not defined as a real number).
is assumed to be the nonnegative numbers, because the square root of a negative number is not defined as a real number).
In Section 1.1 we saw that a function  can be thought of as a machine that takes an input
can be thought of as a machine that takes an input  and produces an output
and produces an output 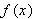 . Similarly, we can think of
. Similarly, we can think of  as a machine that takes an input
as a machine that takes an input 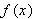 and produces an output
and produces an output  .
.
 can be thought of as a machine that takes an input
can be thought of as a machine that takes an input  and produces an output
and produces an output 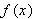 . Similarly, we can think of
. Similarly, we can think of  as a machine that takes an input
as a machine that takes an input 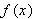 and produces an output
and produces an output  .
.
|
|
The procedure for finding a formula for an inverse function can be described as follows:
|
|
The Domain and Range of an Inverse Function
The domain and range of a one-to-one function are nicely related to the domain and range of its inverse. To understand this
relationship, consider a one-to-one function  . Note that
. Note that 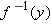 is defined precisely when
is defined precisely when  is in the range of
is in the range of  . Thus the domain of
. Thus the domain of  equals the range of
equals the range of  .
.
 . Note that
. Note that 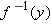 is defined precisely when
is defined precisely when  is in the range of
is in the range of  . Thus the domain of
. Thus the domain of  equals the range of
equals the range of  .
.
Similarly, because  reverses the action of
reverses the action of  , a moment's thought shows that the range of
, a moment's thought shows that the range of  equals the domain of
equals the domain of  . We can summarize the relationship between the domains and ranges of functions and their inverses as follows:
. We can summarize the relationship between the domains and ranges of functions and their inverses as follows:
 reverses the action of
reverses the action of  , a moment's thought shows that the range of
, a moment's thought shows that the range of  equals the domain of
equals the domain of  . We can summarize the relationship between the domains and ranges of functions and their inverses as follows:
. We can summarize the relationship between the domains and ranges of functions and their inverses as follows:
|
||||||||||||||
|
|||||||||||||||||||||||||||||||||||
The Composition of a Function and Its Inverse
The following example will help motivate our next result.
|
Similar equations hold for the composition of any one-to-one function and its inverse:
|
||||||||||||||
To see why these results hold, first suppose  is a number in the range of
is a number in the range of  . Let
. Let 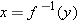 . Then
. Then 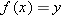 . Thus
. Thus
as claimed above.
 is a number in the range of
is a number in the range of  . Let
. Let 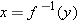 . Then
. Then 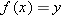 . Thus
. Thus
|
To verify the second conclusion in the box above, suppose  is a number in the domain of
is a number in the domain of  . Let
. Let 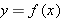 . Then
. Then 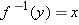 . Thus
. Thus
as claimed.
 is a number in the domain of
is a number in the domain of  . Let
. Let 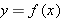 . Then
. Then 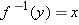 . Thus
. Thus
|
Recall that 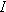 is the identity function defined by
is the identity function defined by 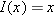 (where we have left the domain vague), or we could equally well define
(where we have left the domain vague), or we could equally well define 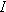 by the equation
by the equation 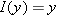 . The results in the box above could be expressed by the equations
. The results in the box above could be expressed by the equations
Here the 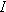 in the first equation above has domain equal to the range of
in the first equation above has domain equal to the range of  (which equals the domain of
(which equals the domain of  ), and the
), and the 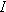 in the second equation above has the same domain as
in the second equation above has the same domain as  . The equations above explain why the terminology “inverse” is used for the inverse function:
. The equations above explain why the terminology “inverse” is used for the inverse function:  is the inverse of
is the inverse of  under composition in the sense that the composition of
under composition in the sense that the composition of  and
and  in either order gives the identity function.
in either order gives the identity function.
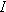 is the identity function defined by
is the identity function defined by 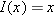 (where we have left the domain vague), or we could equally well define
(where we have left the domain vague), or we could equally well define 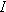 by the equation
by the equation 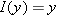 . The results in the box above could be expressed by the equations
. The results in the box above could be expressed by the equations
|
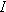 in the first equation above has domain equal to the range of
in the first equation above has domain equal to the range of  (which equals the domain of
(which equals the domain of  ), and the
), and the 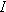 in the second equation above has the same domain as
in the second equation above has the same domain as  . The equations above explain why the terminology “inverse” is used for the inverse function:
. The equations above explain why the terminology “inverse” is used for the inverse function:  is the inverse of
is the inverse of  under composition in the sense that the composition of
under composition in the sense that the composition of  and
and  in either order gives the identity function.
in either order gives the identity function.
The figure below illustrates the equation 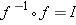 , thinking of
, thinking of  and
and  as machines.
as machines.
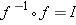 , thinking of
, thinking of  and
and  as machines.
as machines.
|
|
|
|
We start with
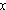 as the input. The first machine produces output as the input. The first machine produces output 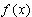 , which then becomes the input for the second machine. When , which then becomes the input for the second machine. When 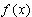 is input into the second machine, the output is is input into the second machine, the output is 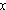 because the second machine, which is based on because the second machine, which is based on 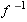 , reverses the action of , reverses the action of 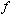 . .
|
Suppose you need to compute the inverse of a function  . As discussed earlier, to find a formula for
. As discussed earlier, to find a formula for  you need to solve the equation
you need to solve the equation 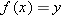 for
for  in terms of
in terms of  . Once you have obtained a formula for
. Once you have obtained a formula for  , a good way to check your result is to verify one or both of the equations in the box above.
, a good way to check your result is to verify one or both of the equations in the box above.
 . As discussed earlier, to find a formula for
. As discussed earlier, to find a formula for  you need to solve the equation
you need to solve the equation 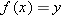 for
for  in terms of
in terms of  . Once you have obtained a formula for
. Once you have obtained a formula for  , a good way to check your result is to verify one or both of the equations in the box above.
, a good way to check your result is to verify one or both of the equations in the box above.
|
Comments About Notation
The notation 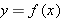 leads naturally to the notation
leads naturally to the notation 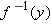 . Recall, however, that in defining a function the variable is simply a placeholder. Thus we could use other letters, including
. Recall, however, that in defining a function the variable is simply a placeholder. Thus we could use other letters, including
 , as the variable for the inverse function. For example, consider the function
, as the variable for the inverse function. For example, consider the function  , with domain equal to the set of positive numbers, defined by the equation
, with domain equal to the set of positive numbers, defined by the equation
As we know, the inverse function is given by the formula
However, the inverse function could also be characterized by the formula
Other letters could also be used as the placeholder. For example, we might also characterize the inverse function by the formula
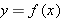 leads naturally to the notation
leads naturally to the notation 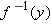 . Recall, however, that in defining a function the variable is simply a placeholder. Thus we could use other letters, including
. Recall, however, that in defining a function the variable is simply a placeholder. Thus we could use other letters, including
 , as the variable for the inverse function. For example, consider the function
, as the variable for the inverse function. For example, consider the function  , with domain equal to the set of positive numbers, defined by the equation
, with domain equal to the set of positive numbers, defined by the equation
|
|
|
|
The notation  for the inverse of a function (which means the inverse under composition) should not be confused with the multiplicative
inverse
for the inverse of a function (which means the inverse under composition) should not be confused with the multiplicative
inverse 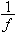 . In other words,
. In other words, 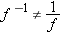 . However, if the exponent
. However, if the exponent 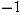 is placed anywhere other than immediately after a function symbol, then it should probably be interpreted as a multiplicative
inverse.
is placed anywhere other than immediately after a function symbol, then it should probably be interpreted as a multiplicative
inverse.
 for the inverse of a function (which means the inverse under composition) should not be confused with the multiplicative
inverse
for the inverse of a function (which means the inverse under composition) should not be confused with the multiplicative
inverse 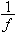 . In other words,
. In other words, 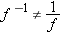 . However, if the exponent
. However, if the exponent 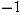 is placed anywhere other than immediately after a function symbol, then it should probably be interpreted as a multiplicative
inverse.
is placed anywhere other than immediately after a function symbol, then it should probably be interpreted as a multiplicative
inverse.
|
|
||||||||||||||||||||||||||||||
When dealing with real-world problems, you may want to choose the notation to reflect the context. The next example illustrates
this idea, with the use of the variable 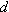 to denote distance and
to denote distance and 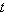 to denote time.
to denote time.
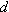 to denote distance and
to denote distance and 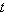 to denote time.
to denote time.
|
||||||||||||||||||||||||||
| EXERCISES | |
For Exercises 1-8, check your answer by evaluating the appropriate function at your answer.
| 1 |
Suppose
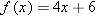 . Evaluate . Evaluate 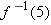 . .
|
| 2 |
Suppose
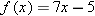 . Evaluate . Evaluate 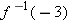 . .
|
| 3 |
Suppose
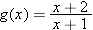 . Evaluate . Evaluate 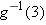 . .
|
| 4 |
Suppose
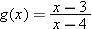 . Evaluate . Evaluate 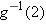 . .
|
| 5 |
Suppose
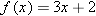 . Find a formula for . Find a formula for  . .
|
| 6 |
Suppose
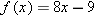 . Find a formula for . Find a formula for  . .
|
| 7 |
Suppose
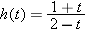 . Find a formula for . Find a formula for 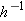 . .
|
| 8 |
Suppose
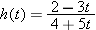 . Find a formula for . Find a formula for 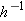 . .
|
| 9 |
Suppose
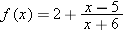 . .
|
| 10 |
Suppose
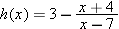 . .
|
| 11 |
Suppose
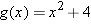 , with the domain of , with the domain of 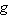 being the set of positive numbers. Evaluate being the set of positive numbers. Evaluate 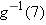 . .
|
| 12 |
Suppose
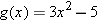 , with the domain of , with the domain of 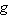 being the set of positive numbers. Evaluate being the set of positive numbers. Evaluate 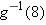 . .
|
| 13 |
Suppose
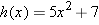 , where the domain of , where the domain of 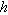 is the set of positive numbers. Find a formula for is the set of positive numbers. Find a formula for 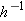 . .
|
| 14 |
Suppose
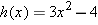 , where the domain of , where the domain of 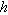 is the set of positive numbers. Find a formula for is the set of positive numbers. Find a formula for 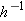 . .
|
For each of the functions  given in Exercises 15-24:
given in Exercises 15-24:
You can check your solutions to part (c) by verifying that 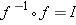 and
and 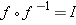 (recall that
(recall that 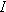 is the function defined by
is the function defined by 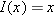 ).
).
 given in Exercises 15-24:
given in Exercises 15-24:
|
|||||||||||||||||||||
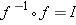 and
and 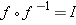 (recall that
(recall that 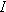 is the function defined by
is the function defined by 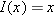 ).
).
| 15 |
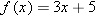 |
| 16 |
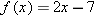 |
| 17 |
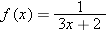 |
| 18 |
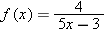 |
| 19 |
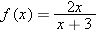 |
| 20 |
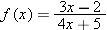 |
| 21 |
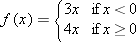 |
| 22 |
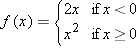 |
| 23 |
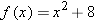 , where the domain of , where the domain of  equals equals 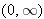 . .
|
| 24 |
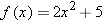 , where the domain of , where the domain of  equals equals 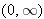 . .
|
| 25 |
Suppose
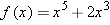 . Which of the numbers listed below equals . Which of the numbers listed below equals 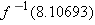 ? ?
[For this particular function, it is not possible to find a formula for
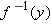 .] .]
|
| 26 |
Suppose
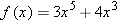 . Which of the numbers listed below equals . Which of the numbers listed below equals 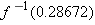 ? ?
[For this particular function, it is not possible to find a formula for
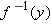 .] .]
|
| 27 |
What is the taxable income of a single person who paid $10,000 in federal taxes for 2011?
|
| 28 |
What is the taxable income of a single person who paid $20,000 in federal taxes for 2011?
|
| 29 |
Suppose
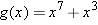 . Evaluate . Evaluate
|
| 30 |
Suppose
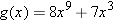 . Evaluate . Evaluate
|
| PROBLEMS | |
| 31 |
The exact number of meters in
 yards is yards is 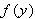 , where , where  is the function defined by is the function defined by
|
| 32 |
The exact number of kilometers in
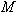 miles is miles is 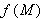 , where , where  is the function defined by is the function defined by
|
| 33 |
A temperature
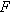 degrees Fahrenheit corresponds to degrees Fahrenheit corresponds to 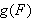 degrees on the Kelvin temperature scale, where degrees on the Kelvin temperature scale, where
|
| 34 |
| 35 |
Suppose
 is the function whose domain is the set of real numbers, with is the function whose domain is the set of real numbers, with  defined on this domain by the formula defined on this domain by the formula
Explain why
 is not a one-to-one function. is not a one-to-one function.
|
| 36 |
Suppose
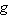 is the function whose domain is the interval is the function whose domain is the interval 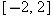 , with , with 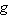 defined on this domain by the formula defined on this domain by the formula
Explain why
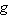 is not a one-to-one function. is not a one-to-one function.
|
| 37 |
Show that if
 is the function defined by is the function defined by 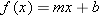 , where , where 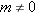 , then , then  is a one-to-one function. is a one-to-one function.
|
| 38 |
Show that if
 is the function defined by is the function defined by 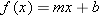 , where , where 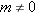 , then the inverse function , then the inverse function  is defined by the formula is defined by the formula 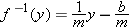 . .
|
| 39 |
Consider the function
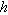 whose domain is the interval whose domain is the interval 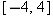 , with , with 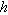 defined on this domain by the formula defined on this domain by the formula
Does
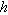 have an inverse? If so, find it, along with its domain and range. If not, explain why not. have an inverse? If so, find it, along with its domain and range. If not, explain why not.
|
| 40 |
Consider the function
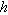 whose domain is the interval whose domain is the interval 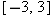 , with , with 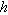 defined on this domain by the formula defined on this domain by the formula
Does
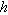 have an inverse? If so, find it, along with its domain and range. If not, explain why not. have an inverse? If so, find it, along with its domain and range. If not, explain why not.
|
| 41 |
Suppose
 is a one-to-one function. Explain why the inverse of the inverse of is a one-to-one function. Explain why the inverse of the inverse of  equals equals  . In other words, explain why . In other words, explain why
|
| 42 |
The function
 defined by defined by
 is the set of real numbers). Compute is the set of real numbers). Compute 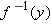 for four different values of for four different values of  of your choice. of your choice.
[For this particular function, it is not possible to find a formula for
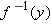 .] .]
|
| 43 |
Suppose
 is a function whose domain equals is a function whose domain equals 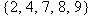 and whose range equals and whose range equals 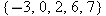 . Explain why . Explain why  is a one-to-one function. is a one-to-one function.
|
| 44 |
Suppose
 is a function whose domain equals is a function whose domain equals 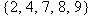 and whose range equals and whose range equals 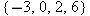 . Explain why . Explain why  is not a one-to-one function. is not a one-to-one function.
|
| 45 |
Show that the composition of two one-to-one functions is a one-to-one function.
|
| 46 |
Give an example to show that the sum of two one-to-one functions is not necessarily a one-to-one function.
|
| 47 |
Give an example to show that the product of two one-to-one functions is not necessarily a one-to-one function.
|
| 48 |
Give an example of a function
 such that the domain of such that the domain of  and the range of and the range of  both equal the set of integers, but both equal the set of integers, but  is not a one-to-one function. is not a one-to-one function.
|
| 49 |
Give an example of a one-to-one function whose domain equals the set of integers and whose range equals the set of positive
integers.
|
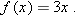
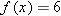 .
.
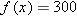 .
.
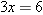 for
for 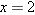 .
.
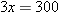 for
for 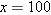 .
.
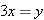 for
for 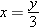 .
.
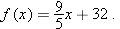
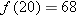 , this formula shows that
, this formula shows that 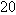 degrees Celsius corresponds to
degrees Celsius corresponds to 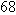 degrees Fahrenheit.
degrees Fahrenheit.
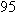 degrees Fahrenheit to the Celsius scale.
degrees Fahrenheit to the Celsius scale.
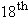 century by the German physicist and engineer Daniel Gabriel Fahrenheit.
century by the German physicist and engineer Daniel Gabriel Fahrenheit.
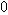 as the boiling point of water and
as the boiling point of water and 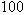 as the freezing point. Later this was reversed, giving us the familiar scale in which higher numbers correspond to hotter
temperatures.
as the freezing point. Later this was reversed, giving us the familiar scale in which higher numbers correspond to hotter
temperatures.
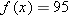 . Solving the equation
. Solving the equation 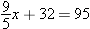 for
for 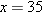 . Thus
. Thus 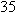 degrees Celsius corresponds to
degrees Celsius corresponds to 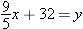
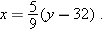
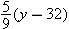 degrees Celsius corresponds to
degrees Celsius corresponds to 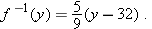
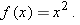
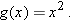
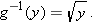
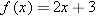 .
.
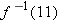 .
.
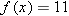 . In other words, we must solve the equation
. In other words, we must solve the equation 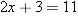 . The solution to this equation is
. The solution to this equation is 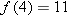 , and hence
, and hence 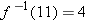 .
.
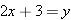
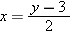 . Thus
. Thus 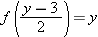 , and hence
, and hence
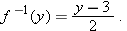

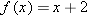
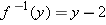
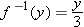
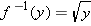
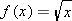
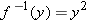

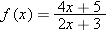
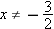 . Find a formula for
. Find a formula for 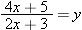
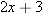 , getting
, getting
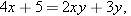
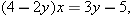
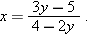
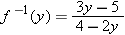
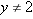 .
.
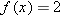 has no solution (try to solve it to see why), and thus
has no solution (try to solve it to see why), and thus 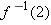 is not defined.
is not defined.
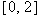 , with
, with 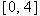 because that interval is equal to the set of squares of numbers in the interval
because that interval is equal to the set of squares of numbers in the interval 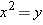 for
for 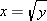 . In other words,
. In other words, 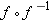 .
.
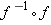 .
.
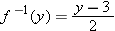 . Thus we have the following:
. Thus we have the following:
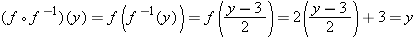
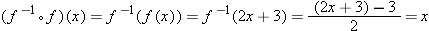
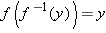 for every
for every 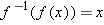 for every
for every 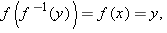
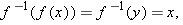
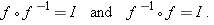

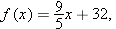
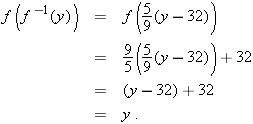
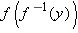 had simplified to anything other than
had simplified to anything other than 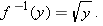
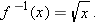
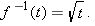
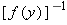 .
.
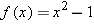 , with the domain of
, with the domain of 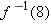 .
.
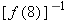 .
.
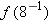 .
.
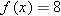 . In other words, we must solve the equation
. In other words, we must solve the equation 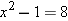 . The solution to this equation is
. The solution to this equation is 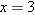 . Thus
. Thus 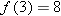 , and hence
, and hence 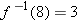 .
.
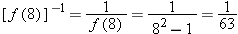
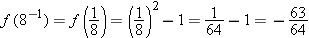
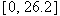 such that
such that 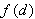 is the number of minutes since the start of the race at which you reached distance
is the number of minutes since the start of the race at which you reached distance 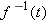 for a number
for a number 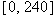 .
.

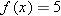 . In other words, we need to solve the equation
. In other words, we need to solve the equation
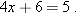
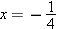 . Thus we have
. Thus we have 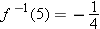 .
.
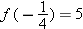 . We have
. We have
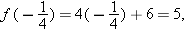
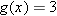 . In other words, we need to solve the equation
. In other words, we need to solve the equation
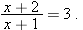
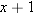 gives the equation
gives the equation
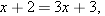
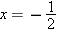 . Thus
. Thus 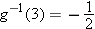 .
.
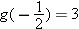 . We have
. We have
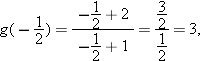
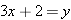
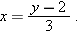
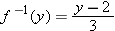
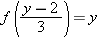 . We have
. We have
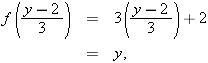
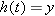 . In other words, we need to solve the equation
. In other words, we need to solve the equation
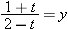
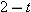 and then collecting all the terms with
and then collecting all the terms with 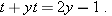
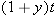 and then dividing both sides by
and then dividing both sides by 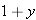 gives
gives
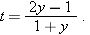
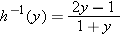
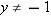 .
.
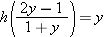 . We have
. We have
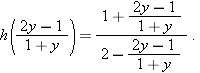
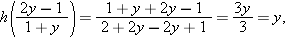
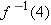 .
.
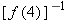 .
.
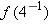 .
.
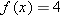 . In other words, we need to solve the equation
. In other words, we need to solve the equation
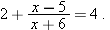
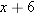 gives the equation
gives the equation
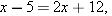
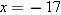 . Thus
. Thus 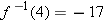 .
.
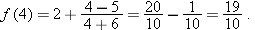
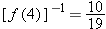 .
.
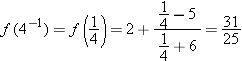
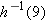 .
.
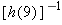 .
.
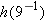 .
.
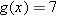 . In other words, we need to find a positive solution to the equation
. In other words, we need to find a positive solution to the equation
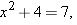
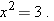
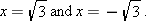
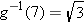 .
.
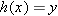 . In other words, we need to solve the equation
. In other words, we need to solve the equation
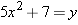
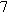 from both sides of the equation above and then dividing both sides by
from both sides of the equation above and then dividing both sides by 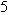 and taking square roots gives
and taking square roots gives
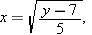
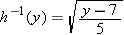
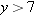 (the restriction that
(the restriction that 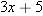 makes sense for all real numbers
makes sense for all real numbers 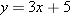
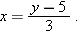
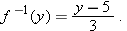
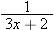 makes sense except when
makes sense except when 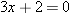 . Solving this equation for
. Solving this equation for 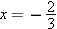 . Thus the domain of
. Thus the domain of 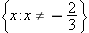 .
.
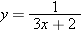
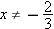 . To solve this equation for
. To solve this equation for 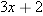 , getting
, getting
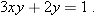
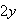 from both sides, then divide by
from both sides, then divide by 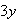 , getting
, getting
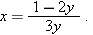
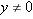 and produces a number
and produces a number 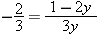 leads to nonsense, as you can verify if you try to solve it for
leads to nonsense, as you can verify if you try to solve it for 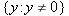 .
.
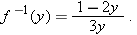
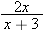 makes sense except when
makes sense except when 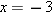 . Thus the domain of
. Thus the domain of 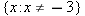 .
.
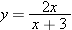
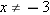 . To solve this equation for
. To solve this equation for 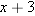 , getting
, getting
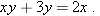
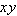 from both sides, getting
from both sides, getting
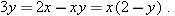
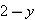 gives
gives
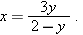
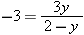 leads to nonsense, as you can verify if you try to solve it for
leads to nonsense, as you can verify if you try to solve it for 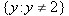 .
.
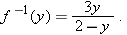
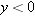 , then
, then 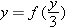 , and if
, and if 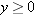 , then
, then 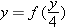 . Thus every real number
. Thus every real number 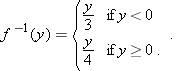
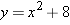
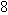 from both sides and then take square roots of both sides, getting
from both sides and then take square roots of both sides, getting
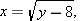
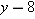 because
because 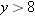 . Thus the range of
. Thus the range of 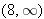 .
.
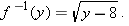
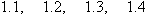
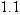 by checking whether or not
by checking whether or not 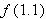 equals
equals 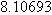 . Using a calculator, we find that
. Using a calculator, we find that
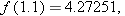
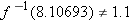 .
.
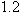 by checking whether or not
by checking whether or not 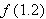 equals
equals 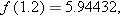
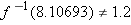 .
.
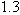 by checking whether or not
by checking whether or not 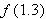 equals
equals 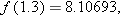
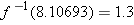 .
.
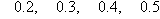
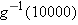 . Letting
. Letting 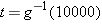 , this means that we need to solve the equation
, this means that we need to solve the equation 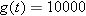 for
for 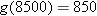 ,
, 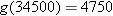 , and
, and 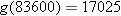 . Because
. Because 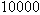 is between
is between 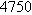 and
and 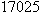 , this means that
, this means that 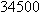 and
and 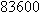 . Thus
. Thus 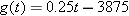 . Solving the equation
. Solving the equation
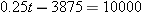
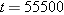 . Thus a single person whose federal tax bill was $10,000 had a taxable income of $55,500.
. Thus a single person whose federal tax bill was $10,000 had a taxable income of $55,500.
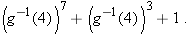
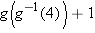 . Because
. Because 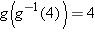 , the quantity above equals
, the quantity above equals 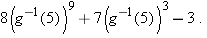
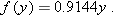
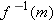 .
.
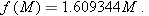
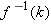 .
.
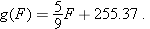
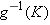 .
.
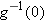 . (This is absolute zero, the lowest possible temperature, because all molecular activity stops at
. (This is absolute zero, the lowest possible temperature, because all molecular activity stops at 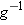 ?
?