Example  17  Hauling a Crate
A flatbed truck is carrying a crate up a hill, as Figure 4.34a illustrates. The coefficient of static friction between the truck bed and the crate is 0.350. Find the maximum acceleration that the truck can attain before the crate begins to slip backward relative to the truck.
Reasoning
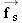
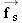
The crate will not slip as long as it has the same acceleration as the truck. Therefore, a net force must act on the crate to accelerate it, and the static frictional force contributes to this net force. Since the crate tends to slip backward, the static frictional force is directed forward, up the hill. As the acceleration of the truck increases, must also increase to produce a corresponding increase in the acceleration of the crate. 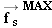However, the static frictional force can increase only until its maximum value is reached, at which point the crate and truck have the maximum acceleration . 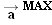If the acceleration increases even more, the crate will slip. 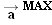To find , we will employ Newton's second law, the definition of weight, and the relationship between the maximum static frictional force and the normal force.
image
Figure 4.34 
(a) A crate on a truck is kept from slipping by the static frictional force . The other forces that act on the crate are its weight and the normal force . (b) The free-body diagram of the crate.
Knowns and Unknowns The data for this problem are as follows:
Description
Symbol
Value
Angle of hill
Coefficient of static friction
0.350
Unknown Variable
    
Maximum acceleration before crate slips
?
Problem-Solving Insight. 
Applications of Newton's second law always involve the net external force, which is the vector sum of all the external forces that act on an object. Each component of the net force leads to a corresponding component of the acceleration.
Modeling the Problem
icon Newton's Second Law ( direction) With the x direction chosen to be parallel to the acceleration of the truck, Newton's second law for this direction can be written as (see Equation 4.2a), where is the net force acting on the crate in the x direction and m is the crate's mass. Using the x components of the forces shown in Figure 4.34b, we find that the net force is . Substituting this expression into Newton's second law gives
The acceleration due to gravity g and the angle are known, but m and are not. We will now turn our attention to finding .
image
icon The Maximum Static Frictional Force The magnitude of the maximum static frictional force is related to the coefficient of static friction and the magnitude of the normal force by Equation 4.7:
  (4.7)
This result can be substituted into Equation 1, as shown at the right. Although is known, is not known. An expression for will be found in Step 3, however.
image
icon Newton's Second Law ( direction) We can determine the magnitude of the normal force by noting that the crate does not accelerate in the y direction . Thus, Newton's second law as given in Equation 4.2b becomes
There are two forces acting on the crate in the y direction (see Figure 4.34b): the normal force and the y component of the weight . (The minus sign is included because this component points along the negative y direction.) Thus, the net force is . Newton's second law becomes
This result for can be substituted into Equation 4.7, as indicated at the right.
image
Solution
Algebraically combining the results of the three steps, we find that
image
Note that the mass m of the crate is algebraically eliminated from the final result. Thus, the maximum acceleration is
Related Homework: Problems 50, 81, 85


Copyright © 2012 John Wiley & Sons, Inc. All rights reserved.