| 4-2 | Average Velocity and Instantaneous Velocity |
|
Learning Objectives
After reading this module, you should be able to …
|
||||||||||||||||||
|
Key Ideas
|
||||||||||||||||||||
Average Velocity and Instantaneous Velocity
If a particle moves from one point to another, we might need to know how fast it moves. Just as in Chapter 2, we can define two quantities that deal with “how fast”: average velocity and instantaneous velocity. However, here we must consider these quantities as vectors and use vector notation.
If a particle moves through a displacement 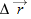 in a time interval
in a time interval  , then its average velocity
, then its average velocity  is
is
or
This tells us that the direction of  (the vector on the left side of Eq. 4-8) must be the same as that of the displacement
(the vector on the left side of Eq. 4-8) must be the same as that of the displacement 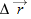 (the vector on the right side). Using Eq. 4-4, we can write Eq. 4-8 in vector components as
(the vector on the right side). Using Eq. 4-4, we can write Eq. 4-8 in vector components as
For example, if a particle moves through displacement  in 2.0 s, then its average velocity during that move is
in 2.0 s, then its average velocity during that move is
That is, the average velocity (a vector quantity) has a component of  along the x axis and a component of
along the x axis and a component of  along the z axis.
along the z axis.
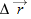 in a time interval
in a time interval  , then its average velocity
, then its average velocity  is
is
|
|
|
 (the vector on the left side of Eq. 4-8) must be the same as that of the displacement
(the vector on the left side of Eq. 4-8) must be the same as that of the displacement 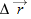 (the vector on the right side). Using Eq. 4-4, we can write Eq. 4-8 in vector components as
(the vector on the right side). Using Eq. 4-4, we can write Eq. 4-8 in vector components as
|
|
 in 2.0 s, then its average velocity during that move is
in 2.0 s, then its average velocity during that move is
|
 along the x axis and a component of
along the x axis and a component of  along the z axis.
along the z axis.
When we speak of the velocity of a particle, we usually mean the particle's instantaneous velocity  at some instant. This
at some instant. This  is the value that
is the value that  approaches in the limit as we shrink the time interval
approaches in the limit as we shrink the time interval  to 0 about that instant. Using the language of calculus, we may write
to 0 about that instant. Using the language of calculus, we may write  as the derivative
as the derivative
 at some instant. This
at some instant. This  is the value that
is the value that  approaches in the limit as we shrink the time interval
approaches in the limit as we shrink the time interval  to 0 about that instant. Using the language of calculus, we may write
to 0 about that instant. Using the language of calculus, we may write  as the derivative
as the derivative
|
|
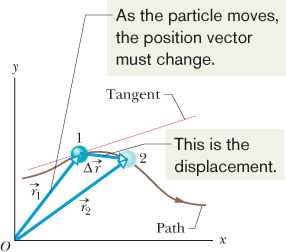
Figure 4-3 shows the path of a particle that is restricted to the  plane. As the particle travels to the right along the curve, its position vector sweeps to the right. During time interval
plane. As the particle travels to the right along the curve, its position vector sweeps to the right. During time interval
 , the position vector changes from
, the position vector changes from 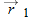 to
to 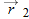 and the particle's displacement is
and the particle's displacement is 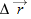 .
.
 plane. As the particle travels to the right along the curve, its position vector sweeps to the right. During time interval
plane. As the particle travels to the right along the curve, its position vector sweeps to the right. During time interval
 , the position vector changes from
, the position vector changes from 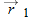 to
to 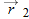 and the particle's displacement is
and the particle's displacement is 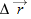 .
.
|
||||
|
||||
To find the instantaneous velocity of the particle at, say, instant t1 (when the particle is at position 1), we shrink interval  to 0 about t1. Three things happen as we do so. (1) Position vector
to 0 about t1. Three things happen as we do so. (1) Position vector 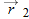 in Fig. 4-3 moves toward
in Fig. 4-3 moves toward 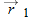 so that
so that 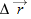 shrinks toward zero.
shrinks toward zero.  The direction of
The direction of  (and thus of
(and thus of  ) approaches the direction of the line tangent to the particle's path at position 1. (3) The average velocity
) approaches the direction of the line tangent to the particle's path at position 1. (3) The average velocity  approaches the instantaneous velocity
approaches the instantaneous velocity  at t1.
at t1.
 to 0 about t1. Three things happen as we do so. (1) Position vector
to 0 about t1. Three things happen as we do so. (1) Position vector 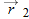 in Fig. 4-3 moves toward
in Fig. 4-3 moves toward 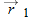 so that
so that 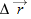 shrinks toward zero.
shrinks toward zero.  The direction of
The direction of  (and thus of
(and thus of  ) approaches the direction of the line tangent to the particle's path at position 1. (3) The average velocity
) approaches the direction of the line tangent to the particle's path at position 1. (3) The average velocity  approaches the instantaneous velocity
approaches the instantaneous velocity  at t1.
at t1.
In the limit as  , we have
, we have  and, most important here,
and, most important here,  takes on the direction of the tangent line. Thus,
takes on the direction of the tangent line. Thus,  has that direction as well:
has that direction as well:
The result is the same in three dimensions:  is always tangent to the particle's path.
is always tangent to the particle's path.
 , we have
, we have  and, most important here,
and, most important here,  takes on the direction of the tangent line. Thus,
takes on the direction of the tangent line. Thus,  has that direction as well:
has that direction as well:

The direction of the instantaneous velocity
 of a particle is always tangent to the particle's path at the particle's position. of a particle is always tangent to the particle's path at the particle's position.
|
 is always tangent to the particle's path.
is always tangent to the particle's path.
To write Eq. 4-10 in unit-vector form, we substitute for 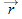 from Eq. 4-1:
from Eq. 4-1:
This equation can be simplified somewhat by writing it as
where the scalar components of  are
are
For example,  is the scalar component of
is the scalar component of  along the x axis. Thus, we can find the scalar components of
along the x axis. Thus, we can find the scalar components of  by differentiating the scalar components of
by differentiating the scalar components of 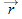 .
.
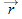 from Eq. 4-1:
from Eq. 4-1:
|
|
|
 are
are
|
|
 is the scalar component of
is the scalar component of  along the x axis. Thus, we can find the scalar components of
along the x axis. Thus, we can find the scalar components of  by differentiating the scalar components of
by differentiating the scalar components of 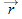 .
.
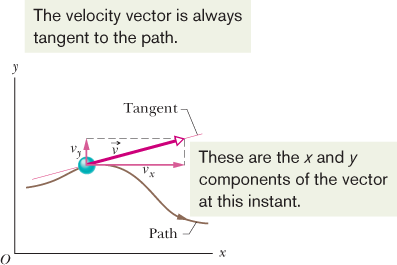
Figure 4-4 shows a velocity vector  and its scalar x and y components. Note that
and its scalar x and y components. Note that  is tangent to the particle's path at the particle's position. Caution: When a position vector is drawn, as in Figs. 4-1 through 4-3, it is an arrow that extends from one point (a “here”) to another point (a “there”). However, when a velocity vector is drawn,
as in Fig. 4-4, it does not extend from one point to another. Rather, it shows the instantaneous direction of travel of a particle at the tail, and its
length (representing the velocity magnitude) can be drawn to any scale.
is tangent to the particle's path at the particle's position. Caution: When a position vector is drawn, as in Figs. 4-1 through 4-3, it is an arrow that extends from one point (a “here”) to another point (a “there”). However, when a velocity vector is drawn,
as in Fig. 4-4, it does not extend from one point to another. Rather, it shows the instantaneous direction of travel of a particle at the tail, and its
length (representing the velocity magnitude) can be drawn to any scale.
 and its scalar x and y components. Note that
and its scalar x and y components. Note that  is tangent to the particle's path at the particle's position. Caution: When a position vector is drawn, as in Figs. 4-1 through 4-3, it is an arrow that extends from one point (a “here”) to another point (a “there”). However, when a velocity vector is drawn,
as in Fig. 4-4, it does not extend from one point to another. Rather, it shows the instantaneous direction of travel of a particle at the tail, and its
length (representing the velocity magnitude) can be drawn to any scale.
is tangent to the particle's path at the particle's position. Caution: When a position vector is drawn, as in Figs. 4-1 through 4-3, it is an arrow that extends from one point (a “here”) to another point (a “there”). However, when a velocity vector is drawn,
as in Fig. 4-4, it does not extend from one point to another. Rather, it shows the instantaneous direction of travel of a particle at the tail, and its
length (representing the velocity magnitude) can be drawn to any scale.
|
||||
|
||||
 Checkpoint 1 Checkpoint 1
|
|
Sample Problem 4.02
Two-dimensional velocity, rabbit run
|
||||||||||||||||||||||||||||
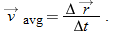
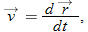
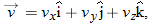
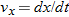 ,
, 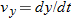 , and
, and 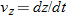 .
.

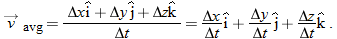
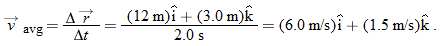
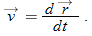
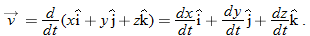
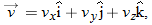
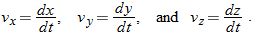
 , through which quadrant is the particle moving at that instant if it is traveling (a) clockwise and (b) counterclockwise
around the circle? For both cases, draw
, through which quadrant is the particle moving at that instant if it is traveling (a) clockwise and (b) counterclockwise
around the circle? For both cases, draw 

 Two-dimensional velocity, rabbit run
Two-dimensional velocity, rabbit run .
.
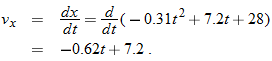
 . Similarly, applying the
. Similarly, applying the 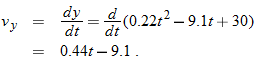
 . Equation
. Equation 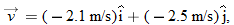
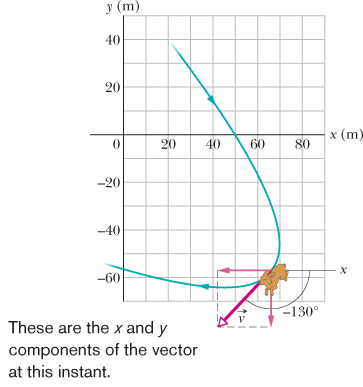
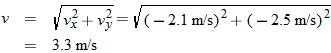
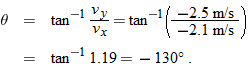
 or
or  ?
?