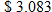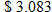|
SECTION 3.6 |
Modeling Functions Using Variation |
| ||||||||||||||||||||||||||||||||

In this section we discuss mathematical models for different applications. Two quantities in the real world often vary with respect to one another. Sometimes, they vary directly. For example, the more money we make, the more total dollars of federal income tax we expect to pay. Sometimes, quantities vary inversely. For example, when interest rates on mortgages decrease, we expect the number of homes purchased to increase because a buyer can afford “more house” with the same mortgage payment when rates are lower. In this section we discuss quantities varying directly, inversely, and jointly.
Direct Variation
When one quantity is a constant multiple of another quantity, we say that the quantities are directly proportional to one another.
| |||||||||||||||||||
In 2005, the national average cost of residential electricity was 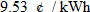 (cents per kilowatt-hour). For example, if a residence used 3400 kWh, then the bill would be
(cents per kilowatt-hour). For example, if a residence used 3400 kWh, then the bill would be 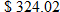 , and if a residence used 2500 kWh, then the bill would be
, and if a residence used 2500 kWh, then the bill would be 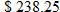 .
.
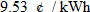 (cents per kilowatt-hour). For example, if a residence used 3400 kWh, then the bill would be
(cents per kilowatt-hour). For example, if a residence used 3400 kWh, then the bill would be 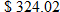 , and if a residence used 2500 kWh, then the bill would be
, and if a residence used 2500 kWh, then the bill would be 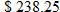 .
.
|
Not all variation we see in nature is direct variation. Isometric growth, where the various parts of an organism grow in direct proportion to each other, is rare in living organisms. If organisms grew isometrically, young children would look just like adults, only smaller. In contrast, most organisms grow nonisometrically; the various parts of organisms do not increase in size in a one-to-one ratio. The relative proportions of a human body change dramatically as the human grows. Children have proportionately larger heads and shorter legs than adults. Allometric growth is the pattern of growth whereby different parts of the body grow at different rates with respect to each other. Some human body characteristics vary directly, and others can be mathematically modeled by direct variation with powers.
| |||||||||||||||||||
One example of direct variation with powers is height and weight of humans. Weight (in pounds) is directly proportional to the cube of height (feet).
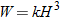
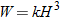
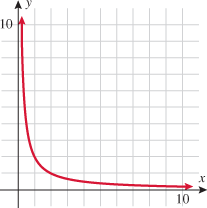
Inverse Variation
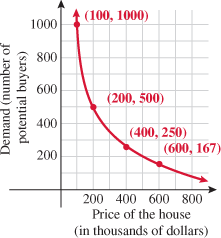
Two fundamental topics covered in economics are supply and demand. Supply is the quantity that producers are willing to sell at a given price. For example, an artist may be willing to paint and sell 5 portraits if each sells for 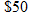 , but that same artist may be willing to sell 100 portraits if each sells for
, but that same artist may be willing to sell 100 portraits if each sells for 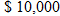 . Demand is the quantity of a good that consumers are not only willing to purchase but also have the capacity to buy at a given price. For example, consumers may purchase 1 billion Big Macs from McDonald's every year, but perhaps only 1 million filet mignons are sold at Outback. There may be 1 billion people who want to buy the filet mignon but don't have the financial means to do so. Economists study the equilibrium between supply and demand.
. Demand is the quantity of a good that consumers are not only willing to purchase but also have the capacity to buy at a given price. For example, consumers may purchase 1 billion Big Macs from McDonald's every year, but perhaps only 1 million filet mignons are sold at Outback. There may be 1 billion people who want to buy the filet mignon but don't have the financial means to do so. Economists study the equilibrium between supply and demand.
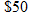 , but that same artist may be willing to sell 100 portraits if each sells for
, but that same artist may be willing to sell 100 portraits if each sells for 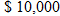 . Demand is the quantity of a good that consumers are not only willing to purchase but also have the capacity to buy at a given price. For example, consumers may purchase 1 billion Big Macs from McDonald's every year, but perhaps only 1 million filet mignons are sold at Outback. There may be 1 billion people who want to buy the filet mignon but don't have the financial means to do so. Economists study the equilibrium between supply and demand.
. Demand is the quantity of a good that consumers are not only willing to purchase but also have the capacity to buy at a given price. For example, consumers may purchase 1 billion Big Macs from McDonald's every year, but perhaps only 1 million filet mignons are sold at Outback. There may be 1 billion people who want to buy the filet mignon but don't have the financial means to do so. Economists study the equilibrium between supply and demand.Demand can be modeled with an inverse variation of price: when the price increases, demand decreases, and vice versa.
| |||||||||||||||||||
|
Two quantities can vary inversely with the 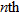 power of
power of 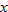 .
.
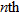 power of
power of 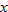 .
.
|
Joint Variation and Combined Variation
We now discuss combinations of variations. When one quantity is proportional to the product of two or more other quantities, the variation is called joint variation. When direct variation and inverse variation occur at the same time, the variation is called combined variation.
An example of a joint variation is simple interest (Section 1.2), which is defined as
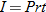 where
where
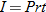
|
|||||||||||||||||
The interest earned is proportional to the product of three quantities (principal, interest rate, and time). Note that if the interest rate increases, then the interest earned also increases. Similarly, if either the initial investment (principal) or the time the money is invested increases, then the interest earned also increases.
An example of combined variation is the combined gas law in chemistry,
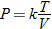 where
where
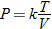
|
|||||||||||||||||
This relation states that the pressure of a gas is directly proportional to the temperature and inversely proportional to the volume containing the gas. For example, as the temperature increases, the pressure increases, but when the volume decreases, pressure increases.
As an example, the gas in the headspace of a soda bottle has a fixed volume. Therefore, as temperature increases, the pressure increases. Compare the different pressures of opening a twist-off cap on a bottle of soda that is cold versus one that is hot. The hot one feels as though it “releases more pressure.”
|
| |||||||||||
| |||||||||||
|
SECTION 3.6 |
EXERCISES |
| SKILLS |
| 1. |
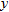 varies directly with varies directly with 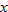 . . |
| 2. | 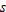 varies directly with varies directly with 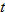 . . |
| 3. |
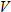 varies directly with varies directly with 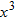 . . |
| 4. | 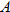 varies directly with varies directly with 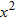 . . |
| 5. |
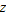 varies directly with varies directly with 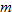 . . |
| 6. | 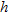 varies directly with varies directly with 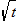 . . |
| 7. |
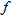 varies inversely with varies inversely with 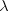 . . |
| 8. | 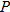 varies inversely with varies inversely with 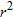 . . |
| 9. |
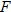 varies directly with varies directly with 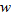 and inversely with and inversely with 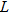 . . |
| 10. | 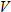 varies directly with varies directly with 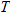 and inversely with and inversely with 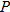 . . |
| 11. |
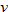 varies directly with both varies directly with both 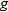 and and 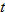 . . |
| 12. | 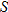 varies directly with both varies directly with both 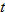 and and 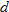 . . |
| 13. |
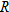 varies inversely with both varies inversely with both 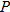 and and 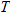 . . |
| 14. | 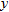 varies inversely with both varies inversely with both 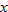 and and 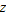 . . |
| 15. |
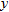 is directly proportional to the square root of is directly proportional to the square root of 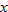 . . |
| 16. | 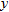 is inversely proportional to the cube of is inversely proportional to the cube of 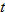 . . |
| 17. |
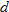 is directly proportional to is directly proportional to 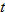 . . 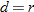 when when 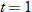 . . |
| 18. | 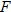 is directly proportional to is directly proportional to 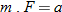 when when 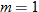 . . |
| 19. |
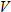 is directly proportional to both is directly proportional to both 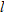 and and 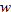 . . 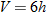 when when 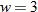 and and 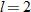 . . |
| 20. | 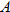 is directly proportional to both is directly proportional to both 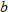 and and 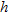 . . 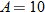 when when 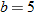 and and 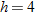 . . |
| 21. |
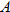 varies directly with the square of varies directly with the square of 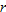 . . 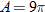 when when 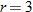 . . |
| 22. | 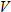 varies directly with the cube of varies directly with the cube of 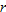 . . 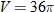 when when 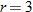 . . |
| 23. |
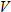 varies directly with both varies directly with both 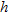 and and 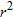 . . 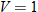 when when 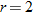 and and 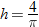 . . |
| 24. | 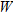 is directly proportional to both is directly proportional to both 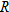 and the square of and the square of 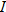 . . 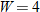 when when 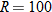 and and 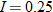 . . |
| 25. |
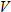 varies inversely with varies inversely with 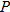 . . 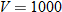 when when 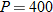 . . |
| 26. | 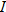 varies inversely with the square of varies inversely with the square of 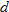 . . 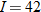 when when 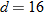 . . |
| 27. |
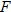 varies inversely with both varies inversely with both 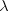 and and 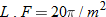 when when 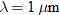 and and 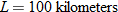 . . |
| 28. | 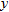 varies inversely with both varies inversely with both 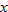 and and 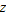 . . 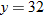 when when 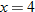 and and 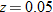 . . |
| 29. |
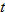 varies inversely with varies inversely with 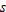 . . 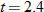 when when 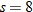 . . |
| 30. | 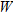 varies inversely with the square of varies inversely with the square of 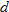 . . 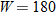 when when 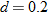 . . |
| 31. |
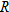 varies inversely with the square of varies inversely with the square of 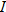 . . 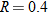 when when 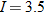 . . |
| 32. | 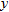 varies inversely with both varies inversely with both 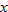 and the square root of and the square root of 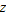 . . 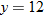 when when 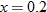 and and 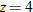 . . |
| 33. |
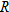 varies directly with varies directly with 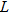 and inversely with and inversely with 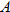 . . 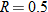 when when 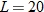 and and 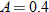 . . |
| 34. | 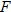 varies directly with varies directly with 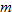 and inversely with and inversely with 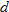 . . 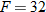 when when 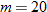 and and 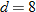 . . |
| 35. |
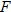 varies directly with both varies directly with both 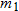 and and 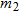 and inversely with the square of and inversely with the square of 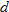 . . 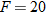 when when 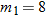 , , 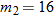 , and , and 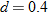 . . |
| 36. | 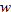 varies directly with the square root of varies directly with the square root of 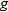 and inversely with the square of and inversely with the square of 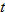 . . 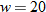 when when 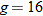 and and 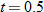 . . |
| APPLICATIONS |
| 37. |
Wages.
Jason and Valerie both work at Panera Bread and have the following paycheck information for a certain week. Find an equation that shows their wages
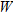 varying directly with the number of hours worked varying directly with the number of hours worked 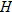 . .
|
| 38. |
Sales Tax.
The sales tax in Orange and Seminole counties in Florida differs by only 0.5%. A new resident knows this but doesn't know which of the counties has the higher tax. The resident lives near the border of the counties and is in the market for a new plasma television and wants to purchase it in the county with the lower tax. If the tax on a pair of
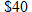 sneakers is sneakers is 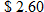 in Orange County and the tax on a in Orange County and the tax on a 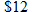 T-shirt is T-shirt is 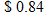 in Seminole County, write two equations: one for each county that describes the tax in Seminole County, write two equations: one for each county that describes the tax 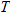 , which is directly proportional to the purchase price , which is directly proportional to the purchase price 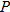 . . |
The ratio of the speed of an object to the speed of sound determines the Mach number. Aircraft traveling at a subsonic speed (less than the speed of sound) have a Mach number less than 1. In other words, the speed of an aircraft is directly proportional to its Mach number. Aircraft traveling at a supersonic speed (greater than the speed of sound) have a Mach number greater than 1. The speed of sound at sea level is approximately 760 miles per hour.
| 39. |
Military.
The U.S. Navy Blue Angels fly F-18 Hornets that are capable of Mach 1.7. How fast can F-18 Hornets fly at sea level?
|
| 40. |
Military.
The U.S. Air Force's newest fighter aircraft is the F-35, which is capable of Mach 1.9. How fast can an F-35 fly at sea level?
|
| 41. |
Human Anatomy.
The length of your forearm 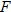 (wrist to elbow) is directly proportional to the length of your hand (wrist to elbow) is directly proportional to the length of your hand 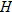 (length from wrist to tip of middle finger). Write the equation that describes this relationship if the length of your forearm is 11 inches and the length of your hand is 6.8 inches. (length from wrist to tip of middle finger). Write the equation that describes this relationship if the length of your forearm is 11 inches and the length of your hand is 6.8 inches.
|
| 42. |
Human Anatomy.
Each section of your index finger, from the tip to the base of the wrist, is larger than the preceding one by about the golden (Fibonacci) ratio. Find an equation that represents the ratio of each section of your finger related to the previous one if one section is eight units long and the next section is five units long.
|
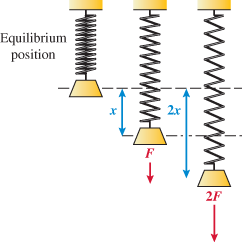
Hooke's law in physics states that if a spring at rest (equilibrium position) has a weight attached to it, then the distance the spring stretches is directly proportional to the force (weight), according to the formula:
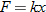 where
where 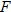 is the force in Newtons (N),
is the force in Newtons (N), 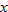 is the distance stretched in meters (m), and
is the distance stretched in meters (m), and 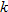 is the spring constant (N/m).
is the spring constant (N/m).
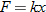
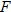 is the force in Newtons (N),
is the force in Newtons (N), 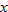 is the distance stretched in meters (m), and
is the distance stretched in meters (m), and 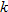 is the spring constant (N/m).
is the spring constant (N/m).
|
| 43. |
Physics.
A force of
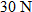 will stretch the spring 10 centimeters. How far will a force of will stretch the spring 10 centimeters. How far will a force of 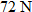 stretch the spring? stretch the spring? |
| 44. |
Physics.
A force of
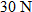 will stretch the spring 10 centimeters. How much force is required to stretch the spring 18 centimeters? will stretch the spring 10 centimeters. How much force is required to stretch the spring 18 centimeters? |
| 45. |
Business.
A cell phone company develops a pay-as-you-go cell phone plan in which the monthly cost varies directly as the number of minutes used. If the company charges
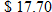 in a month when 236 minutes are used, what should the company charge for a month in which 500 minutes are used? in a month when 236 minutes are used, what should the company charge for a month in which 500 minutes are used? |
| 46. |
Economics.
Demand for a product varies inversely with the price per unit of the product. Demand for the product is 10,000 units when the price is
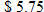 per unit. Find the demand for the product (to the nearest hundred units) when the price is per unit. Find the demand for the product (to the nearest hundred units) when the price is 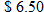 . . |
| 47. |
Sales.
Levi's makes jeans in a variety of price ranges for juniors. The Flare 519 jeans sell for about
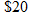 , whereas the 646 Vintage Flare jeans sell for , whereas the 646 Vintage Flare jeans sell for 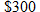 . The demand for Levi's jeans is inversely proportional to the price. If 300,000 pairs of the 519 jeans were bought, approximately how many of the Vintage Flare jeans were bought? . The demand for Levi's jeans is inversely proportional to the price. If 300,000 pairs of the 519 jeans were bought, approximately how many of the Vintage Flare jeans were bought? |
| 48. |
Sales.
Levi's makes jeans in a variety of price ranges for men. The Silver Tab Baggy jeans sell for about
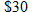 , whereas the Offender jeans sell for about , whereas the Offender jeans sell for about 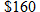 . The demand for Levi's jeans is inversely proportional to the price. If 400,000 pairs of the Silver Tab Baggy jeans were bought, approximately how many of the Offender jeans were bought? . The demand for Levi's jeans is inversely proportional to the price. If 400,000 pairs of the Silver Tab Baggy jeans were bought, approximately how many of the Offender jeans were bought? |
In physics, the inverse square law states that any physical quantity or strength is inversely proportional to the square of the distance from the source of that physical quantity. In particular, the intensity of light radiating from a point source is inversely proportional to the square of the distance from the source. Below is a table of average distances from the Sun:
|
| 49. |
Solar Radiation.
The solar radiation on the Earth is approximately 1400 watts per square meter
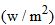 . How much solar radiation is there on Mars? Round to the nearest hundred watts per square meter. . How much solar radiation is there on Mars? Round to the nearest hundred watts per square meter. |
| 50. |
Solar Radiation.
The solar radiation on the Earth is approximately 1400 watts per square meter. How much solar radiation is there on Mercury? Round to the nearest hundred watts per square meter.
|
| 51. |
Investments.
Marilyn receives a
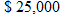 bonus from her company and decides to put the money toward a new car that she will need in two years. Simple interest is directly proportional to the principal and the time invested. She compares two different banks’ rates on money market accounts. If she goes with Bank of America, she will earn bonus from her company and decides to put the money toward a new car that she will need in two years. Simple interest is directly proportional to the principal and the time invested. She compares two different banks’ rates on money market accounts. If she goes with Bank of America, she will earn 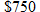 in interest, but if she goes with the Navy Federal Credit Union, she will earn in interest, but if she goes with the Navy Federal Credit Union, she will earn 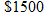 . What is the interest rate on money market accounts at both banks? . What is the interest rate on money market accounts at both banks? |
| 52. |
Investments.
Connie and Alvaro sell their house and buy a fixer-upper house. They made
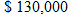 on the sale of their previous home. They know it will take 6 months before the general contractor will start their renovation, and they want to take advantage of a 6-month CD that pays simple interest. What is the rate of the 6-month CD if they will make on the sale of their previous home. They know it will take 6 months before the general contractor will start their renovation, and they want to take advantage of a 6-month CD that pays simple interest. What is the rate of the 6-month CD if they will make 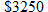 in interest? in interest? |
| 53. |
Chemistry.
A gas contained in a 4 milliliter container at a temperature of
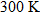 has a pressure of 1 atmosphere. If the temperature decreases to has a pressure of 1 atmosphere. If the temperature decreases to 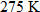 , what is the resulting pressure? , what is the resulting pressure? |
| 54. |
Chemistry.
A gas contained in a 4 milliliter container at a temperature of
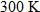 has a pressure of 1 atmosphere. If the container changes to a volume of 3 millileters, what is the resulting pressure? has a pressure of 1 atmosphere. If the container changes to a volume of 3 millileters, what is the resulting pressure? |
| CATCH THE MISTAKE |
| 55. |
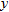 varies directly with varies directly with 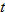 and indirectly with and indirectly with 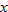 . When . When 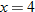 and and 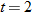 , then , then 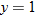 . Find an equation that describes this variation. . Find an equation that describes this variation.Solution:
|
| 56. |
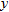 varies directly with varies directly with 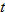 and the square of and the square of 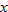 . When . When 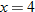 and and 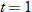 , then , then 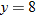 . Find an equation that describes this variation. . Find an equation that describes this variation.Solution:
|
| CONCEPTUAL |
| 57. |
The area of a triangle is directly proportional to both the base and the height of the triangle (joint variation). |
| 58. | Average speed is directly proportional to both distance and time (joint variation). |
| 59. |
Inverse variation
|
| 60. | Direct variation
|
| CHALLENGE |
The three parameters that help classify the strength of optical turbulence are:
The variance of the irradiance of a laser 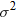 is directly proportional to
is directly proportional to 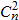 ,
, 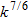 , and
, and 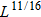 .
.
|
|||||||||||||
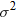 is directly proportional to
is directly proportional to 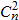 ,
, 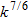 , and
, and 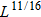 .
.| 61. |
When
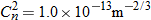 , , 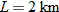 , and , and 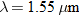 , the variance of irradiance for a plane wave , the variance of irradiance for a plane wave 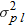 is 7.1. Find the equation that describes this variation. is 7.1. Find the equation that describes this variation. |
| 62. | When
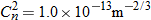 , , 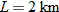 , and , and 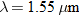 , the variance of irradiance for a spherical wave , the variance of irradiance for a spherical wave 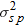 is 2.3. Find the equation that describes this variation. is 2.3. Find the equation that describes this variation. |
| TECHNOLOGY |
Data from 1995 to 2006 for oil prices in dollars per barrel, the U.S. Dow Jones Utilities Stock Index, New Privately Owned Housing, and 5-year Treasury Constant Maturity Rate are given in the table. (Data are from Forecast Center's Historical Economic and Market Home Page at www.neatideas.com/djutil.htm.)
Use the calculator 
 commands to enter the table with
commands to enter the table with  as the oil price,
as the oil price,  as the utilities stock index,
as the utilities stock index,  as number of housing units, and
as number of housing units, and  as the 5-year maturity rate.
as the 5-year maturity rate.
 commands to enter the table with
commands to enter the table with 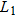 as the oil price,
as the oil price, 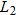 as the utilities stock index,
as the utilities stock index, 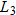 as number of housing units, and
as number of housing units, and 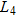 as the 5-year maturity rate.
as the 5-year maturity rate.
|
| 63. | An increase in oil price in dollars per barrel will drive the U.S. Dow Jones Utilities Stock Index to soar.
|
| 64. | An increase in oil price in dollars per barrel will affect the interest rates across the board—in particular, the 5-year Treasury constant maturity rate.
|
| 65. | An increase in interest rates—in particular, the 5-year Treasury constant maturity rate—will affect the number of new, privately owned housing units.
|
| 66. | An increase in the number of new, privately owned housing units will affect the U.S. Dow Jones Utilities Stock Index.
|
Data for retail gasoline price in dollars per gallon for the period March 2000 to March 2008 are given in the following table. (Data are from Energy Information Administration, Official Energy Statistics from the U.S. government at http://tonto.eia.doe.gov/oog/info/gdu/gaspump.html.) Use the calculator 
 command to enter the table below with
command to enter the table below with 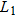 as the year (
as the year (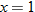 for year 2000) and
for year 2000) and  as the gasoline price in dollars per gallon.
as the gasoline price in dollars per gallon.
 command to enter the table below with
command to enter the table below with  as the year (
as the year (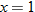 for year 2000) and
for year 2000) and 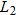 as the gasoline price in dollars per gallon.
as the gasoline price in dollars per gallon.
|
| 67. |
|
| 68. |
|
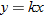 , where
, where 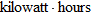 (kWh) used. If a household in Tennessee on average used
(kWh) used. If a household in Tennessee on average used 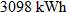 per month and had an average monthly electric bill of
per month and had an average monthly electric bill of 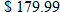 , find a mathematical model that gives the cost of electricity in Tennessee in terms of the number of
, find a mathematical model that gives the cost of electricity in Tennessee in terms of the number of 
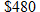 .
.
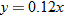 ; the cost of electricity in California is
; the cost of electricity in California is 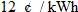 .
.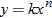 , where
, where 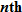
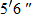 woman weigh who has the same proportionality as the male?
woman weigh who has the same proportionality as the male?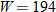 and
and 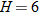 into
into 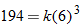
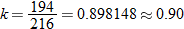
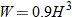
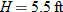 .
.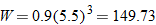
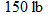 .
.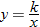 , where
, where  million house?
million house?

 Technology Tip
Technology Tip
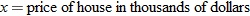
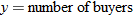
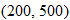
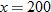 and
and 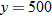 into
into 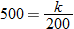
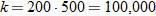
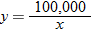
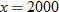 .
.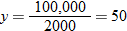
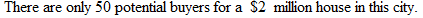
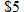 million condominium?
million condominium?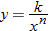 , then we say that
, then we say that 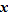 , or
, or 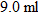 , pressure of 2 atm (atmospheres), and a temperature of
, pressure of 2 atm (atmospheres), and a temperature of 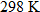 (standard room temperature of
(standard room temperature of 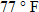 ). If the soda bottle is stored in a refrigerator, the temperature drops to approximately
). If the soda bottle is stored in a refrigerator, the temperature drops to approximately 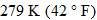 . What is the pressure of the gas in the headspace once the bottle is chilled?
. What is the pressure of the gas in the headspace once the bottle is chilled?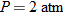 ,
, 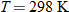 , and
, and 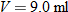 .
.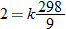
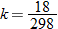
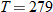 , and
, and 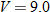 in
in 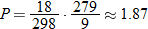
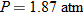
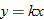

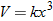
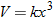
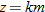
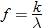
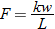
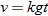
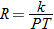
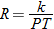
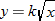
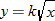
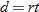
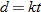 . Using the fact that
. Using the fact that 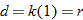 , we see that
, we see that 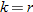 . So,
. So, 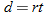 .
.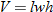
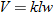 . Using the fact that
. Using the fact that 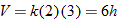 we see that
we see that 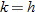 . So,
. So, 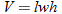 .
.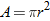
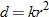 . Using the fact that
. Using the fact that 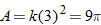 , we see that
, we see that 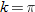 . So,
. So, 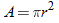 .
.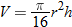
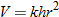 . Using the fact that
. Using the fact that 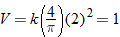 , we see that
, we see that 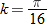 . So,
. So, 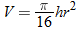 .
.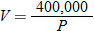
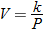 . Using the fact that
. Using the fact that 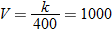 , we see that
, we see that 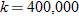 . Hence,
. Hence, 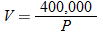 .
.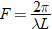
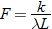 . Using the fact that
. Using the fact that 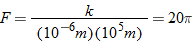 , we see that
, we see that 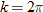 . So,
. So, 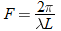 .
.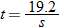
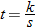 . Using the fact that
. Using the fact that 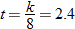 , we see that
, we see that 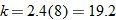 . Hence,
. Hence, 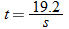 .
.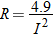
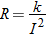 . Using the fact that
. Using the fact that 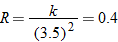 , we see that
, we see that 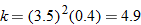 . Hence,
. Hence, 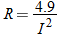 .
.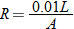
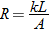 . Using the fact that
. Using the fact that 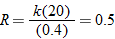 , we see that
, we see that 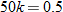 , so that
, so that 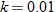 . Hence,
. Hence, 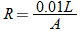 .
.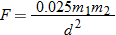
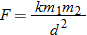 . Using the fact that
. Using the fact that 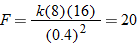 , we see that
, we see that 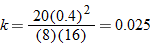 . Hence,
. Hence, 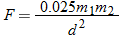 .
.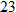
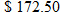
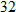
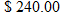
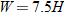
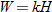 . We need to determine
. We need to determine 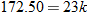 , so that
, so that 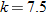 . So,
. So, 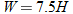 . (Note that Valerie's data also satisfies this equation.)
. (Note that Valerie's data also satisfies this equation.)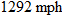
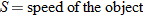 , and
, and 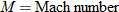 . We are given that
. We are given that 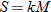 . We also know that when
. We also know that when 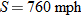 (at sea level),
(at sea level), 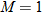 . As such,
. As such, 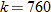 . Hence, for U.S. Navy Blue Angels,
. Hence, for U.S. Navy Blue Angels, 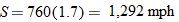 .
.
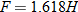
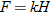 . Using the fact that
. Using the fact that 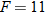 when
when 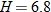 , we see that
, we see that 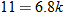 , so that
, so that 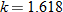 . Hence,
. Hence, 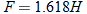 .
.
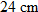
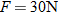 when
when 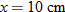 , we see that
, we see that 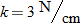 . So,
. So, 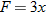 . As such,
. As such, 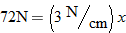 , so that
, so that 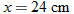 .
.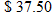
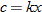 . We must first find
. We must first find 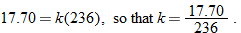
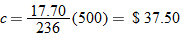
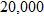
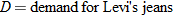 and
and 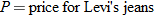 .
.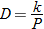 . Using the given information for Flare 519 jeans (namely that
. Using the given information for Flare 519 jeans (namely that 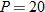 when
when 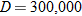 ) yields
) yields 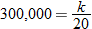 so that
so that 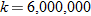 .
.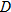 is given by:
is given by: 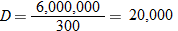 .
.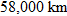
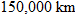
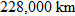
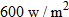
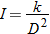 . Using the data for Earth, we obtain:
. Using the data for Earth, we obtain:
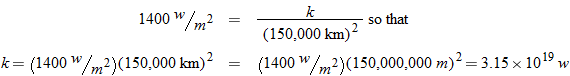
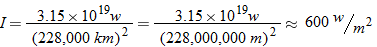
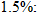 Navy Federal Credit Union:
Navy Federal Credit Union: 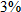
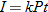 .
.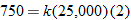 , so that
, so that 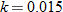 , which corresponds to
, which corresponds to 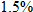 .
.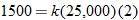 , so that
, so that 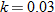 , which corresponds to
, which corresponds to 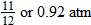
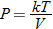 with
with 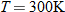 ,
, 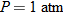 ., and
., and 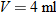 to obtain
to obtain 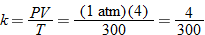 . Thus,
. Thus, 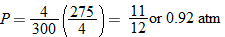 .
.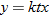
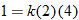
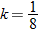
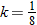 into
into 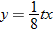
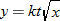
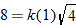
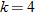
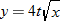
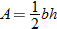 , so area is directly proportional to both base and height.
, so area is directly proportional to both base and height.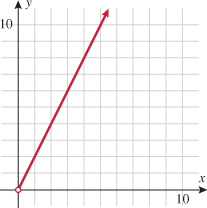
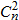 , index of refraction structure parameter
, index of refraction structure parameter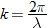
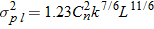
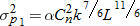 with the following information (all converted to meters):
with the following information (all converted to meters):
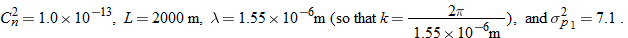
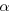 :
:
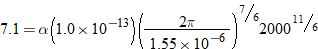
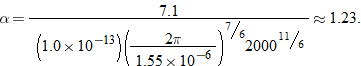
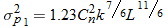 .
.
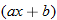 , and
, and  to model the data using the least squares regression. Find the equation of the least-squares regression line using
to model the data using the least squares regression. Find the equation of the least-squares regression line using 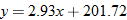 .
.
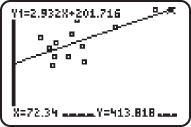
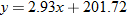 , and is plotted as seen below:
, and is plotted as seen below:

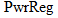 , and
, and 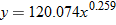 .
.
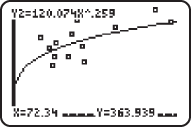
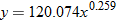 .
.

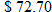 per barrel in September 2006. Which answer is closer to the actual stock index of 417? Round all answers to the nearest whole number.
per barrel in September 2006. Which answer is closer to the actual stock index of 417? Round all answers to the nearest whole number.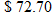 per barrel in September 2006, the predicted stock index from the least-squares regression line is 415 and from the equation of direct variation is 364. The least-squares regression line gives a closer approximation to the actual value, 417.
per barrel in September 2006, the predicted stock index from the least-squares regression line is 415 and from the equation of direct variation is 364. The least-squares regression line gives a closer approximation to the actual value, 417.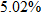 ? Round all answers to two decimal places.
? Round all answers to two decimal places.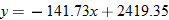 .
.

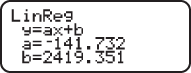
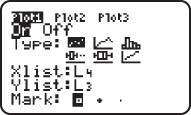


 . The following is the sequence of commands, and screen captures, to use on the
. The following is the sequence of commands, and screen captures, to use on the 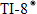 .
.
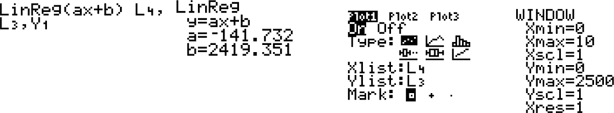

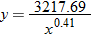 .
.

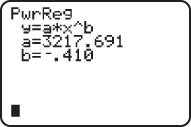
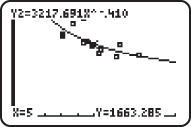
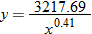 . The following is the sequence of commands, and screen captures, to use on the
. The following is the sequence of commands, and screen captures, to use on the 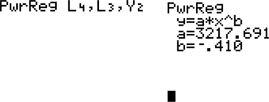

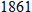 ? Round all answers to the nearest unit.
? Round all answers to the nearest unit.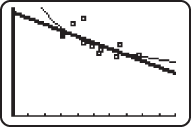
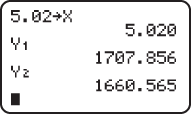
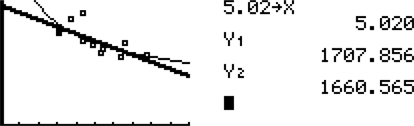
 to model the data using the least-squares regression. Find the equation of the least-squares regression line using
to model the data using the least-squares regression. Find the equation of the least-squares regression line using 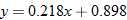
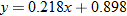
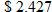 per gallon. Yes, it is very close to the actual price at
per gallon. Yes, it is very close to the actual price at 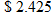 per gallon.
per gallon.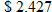 per gallon. Yes, it is very close to the actual price at
per gallon. Yes, it is very close to the actual price at 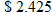 per gallon.
per gallon.