Speed of Sound - Resonance Tube
Objectives
-
•to determine the speed of sound of waves in air
Equipment
-
•resonance tube
-
•tuning forks
-
•rubber mallet
-
•measuring tape
-
•thermometer

Figure 1
Introduction and Theory
A sound wave is a longitudinal wave in which the wave oscillates along the direction of propagation. For a traveling wave of speed v, frequency f, and wavelength λ, the following relationship holds.( 1 )
v = fλ
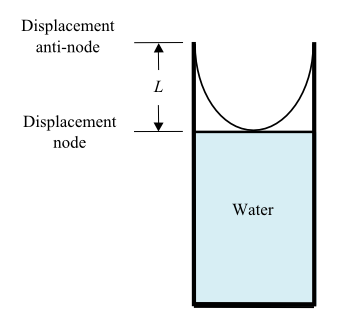
Figure 2: Resonance tube
v = fλ
, the wavelength of the sound wave should also be fixed. As a result the resonance conditions can only be satisfied when the length of the tube L is such that
( 2 )
Ln =
(2n + 1)λ
| 1 |
| 4 |
L =
λ,
which follows from eqn. 2| 1 |
| 4 |
Ln =
(2n + 1)λ
. Fig. 3 shows resonance conditions in which n = 1, 2, and 3. It is easy to notice that | 1 |
| 4 |
L2 − L1 =
λ;
| 1 |
| 2 |
L3 − L2 =
λ.
It can be predicted that the next resonance will occur at | 1 |
| 2 |
L4 =
λ +
λ =
λ
In other words:
| 7 |
| 4 |
| 1 |
| 2 |
| 9 |
| 4 |
( 3 )
Ln + 1 − Ln =
λ
| 1 |
| 2 |
( 4 )
ΔL =
λ
| 1 |
| 2 |
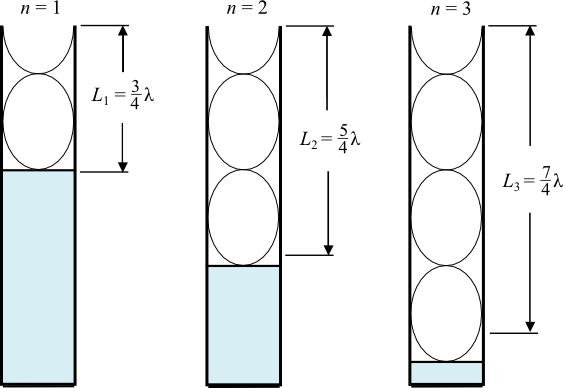
Figure 3: Examples of resonance for n = 1, 2, and 3.
( 5 )
vT = (331.5 + 0.606T) m/s
Procedure
Please print the worksheet for this lab. You will need this sheet to record your data.
Watch the level of water in the side container to avoid overflowing. Be sure to clean up any spills.
1
You will be provided with two tuning forks of known frequencies f. Note that the frequencies of tuning forks are marked on them. Write them down in the Worksheet Lab 10.
2
Fill the tube with water to about 10 cm to the open end of the tube. The level of the water in the tube (= the length of the tube L) can be adjusted by moving the side bucket up and down in the vertical direction.
3
Strike the tuning fork with the rubber head of the mallet for forks with frequencies below 1000 Hz
or with the wooden head for forks with frequencies above 1000 Hz, and place it just above the open end of the tube. Neither the hammer nor the vibrating fork should touch the tube.
4
Find as many resonances as you can for tuning fork one. Repeat your measurements by increasing the water level in the tube. Measure the length of the air column for each resonance from the top edge of the tube. Find the difference in length (ΔL) between the two consecutive resonances to calculate the wavelength of the sound wave. Once the wavelength is determined, the speed of sound follows from eqn. 1v = fλ
(Note the error in the measurement of the length is 1 mm).
5
Repeat step 4 for the other tuning fork with a different frequency.
In the Lab report you will need to calculate the average of the two measured speeds of sound and compare to the theoretical value.
Discussion Questions
What was the purpose of the experiment? What is the theoretical concept that explains the expected experimental results? Where are a node and an antinode occuring in the sound standing wave in this lab experimental set up? Predict the length of the air column where the next resonance will occur. How will the experimental speed change if the temperature in the room is higher? Do the experimental results for the speed of sound in air agree with what is predicted from eqn. 3Ln + 1 − Ln =
λ
within the error? Are the experimental results accurate? Are they precise? Discuss the most probable sources of errors in your measurements. Discuss the major reason for high discrepancy if that's the case.
| 1 |
| 2 |

