Print

Conservation of Mechanical Energy; Work

Purpose

Equipment

  • Dynamics Track Simulation
  • Pencil

Simulation and Tools

Open the Dynamics Track simulation to do this lab. See the Video Overview.

Explore the Apparatus

Open the Dynamics Track. You should be familiar with most of the features of the ramp and cart system from your study of kinematics and dynamics. There are just a few new features that you should familiarize yourself with now.

Setting the Initial Velocity, "V0"

Figures 1 and 3 show parts of the control panel beneath the right end of the track. These controls are used to set the initial velocity of the cart as well as the static and kinetic friction between the cart and track. The panel's appearance changes according to the situation.
the wheels and initial velocity controls, with the wheels radio button selected
Figure 1: Initial Velocity Controls
Clicking the Go button on the left end of the panel gives the cart an inital velocity, v0. "V0" can range from
–300 cm/s
 to
+300 cm/s.
 You can change the direction of the velocity by inserting (or deleting) a – sign, or use the "V0" stepper gadget the stepper gadget, consisting of two stacked buttons, the first with an arrow pointing up, and the second with an arrow pointing down to move through the range of positive and negative velocities.

Adjusting the Kinetic and Static Friction, "μK" and "μS"

By default, the cart runs on frictionless wheels. This is indicated by the selected radio button a selected radio button next to "wheels." To allow you to investigate motion with frictional resistance, the wheels can be replaced by a friction pad with variable friction coefficients—kinetic, "μK," and static, "μS." When the unselected radio button an unselected radio button is clicked, it becomes selected a selected radio button , and the friction pad controls become active, as shown in Figure 3.
two carts: (a) with frictionless wheels, and (b) with a friction pad instead of wheels
Figure 2: Cart Modes
The two left steppers show the default values for "μK" and "μS." These steppers allow you to adjust these two values independently. Well, almost independently. The value of "μK" must remain a respectful amount below "μS." The "μKS?" stepper works similarly to "V0?." The "μKS?" stepper allows you to choose from among several pairs of fixed but unknown (to you) "μK" and "μS" values.
friction pad controls with adjustable static and kinetic friction, with the radio button beside the friction pad label selected
Figure 3: Initial Velocity Controls

Theory

The kinetic energy of a body is the energy associated with its motion.
( 1 )
Kinetic Energy, KE =
1
2
mv2
The potential energy of a physical system is the energy associated with the arrangement of the objects making up the system. This energy is due to the forces among the objects in the system and the work that those forces can do in changing the arrangement of the objects in the system. For example, moving a pair of magnets closer together or farther apart changes the amount of potential energy of the system. In the case of gravitational potential energy for an object near Earth, the energy is due to the force of gravity acting between the objects.
( 2 )
Gravitational Potential Energy, PE = mgh
If an object at some height above the Earth is allowed to fall to a lower altitude, the loss in potential energy of the system of the Earth and the object would be equal to the work done by the force of gravity. In such a case, the motion of the Earth is negligible, and we usually say that it is the falling object that loses the energy. The change in potential energy of the object is given by
( 3 )
ΔPE = PEf − PEo = mghf − mgho,
where h is measured relative to some arbitrary level where we set h = 0. We define the sum of the kinetic energy and the potential energy of an object (or system) as its total mechanical energy. That is,
( 4 )
ME = PE + KE.
Note that energy is a scalar quantity, so v is the speed, which is always positive. And h is the height, which can have a negative sign if an object is below the h = 0 reference level. But this does not represent direction. A swinging pendulum is a good example of a system that undergoes a steady change in PE and KE. As the bob rises, its PE increases, and its KE decreases. As it swings back down, the reverse occurs. If there are no forces other than gravity acting, the decrease in one type of energy is exactly matched by the increase in the other. Thus, the total ME remains constant. If the work on the object by nonconservative forces such as friction is zero, the total mechanical energy will remain constant. For such cases, we can say that mechanical energy is conserved.
Principle of Conservation of Mechanical Energy:

If Wnc = 0, PE0 + KE0 = PEf + KEf, or ΔPE + ΔKE = 0.
A car moving up or down a hill is another example of energy being converted between KE and PE. For a real car, the total mechanical energy would not remain constant, however, since nonconservative forces such as friction are also involved.

Procedure

Please print the worksheet for this lab. You will need this sheet to record your data.

PDF file

I. Conservation of Mechanical Energy

A. Using Conservation of Mechanical Energy to Predict the Change in Height, Δh, of a Cart Traveling up a Frictionless Ramp and Coming to a Halt

Consider a cart traveling up a frictionless ramp. It will start with a certain initial velocity, v0, and a corresponding amount of initial kinetic energy,
1
2
mv02.
 Let's examine this situation with our apparatus. Adjust the ramp angle to 5°. Set "V0" to 160 cm/s. Click the dynamic vectors icon dynamic vectors icon from the Dynamics Track simulation . Click Go and repeat as necessary to observe the following. Note the pink Wx vector (shown as W(x)), which is constant for a given track angle, and always points down the track. This is the component of the weight of the cart acting parallel to the track. As the cart moves, this force does positive or negative work on the cart depending on whether the cart is moving in the direction of the force or opposite it. The green velocity vector varies in magnitude and direction as the cart's kinetic energy changes. So a change in the length of this vector would indicate a ΔKE. When the cart goes up the ramp, Wx and Δx are in opposite directions, so negative work is done to the cart. Going down the ramp, positive work is done to the cart. A much more accessible way to describe this series of events involves replacing the work by gravity with the change in potential energy of the cart. Again, the cart starts with some initial KE0, and we'll arbitrarily set its initial PE0 to zero. As the cart loses KE going up the track, it gains an equal amount of PE. This is reversed on the way back down.
( 5 )
PE0 + KE0 = PEf + KEf
( 6 )
mgh0 +
1
2
mv02 = mghf +
1
2
mvf2
To explore how these equations describe the motion of the cart, you will do the following. Predicted Δh from Conservation of Mechanical Energy The initial kinetic energy, KE0, can be found from the empty cart's mass and its initial speed, which you'll set using the initial velocity "V0" control. The cart mass is 0.250 kg.
1
Set the ramp angle to any angle from +1° to +5°. Record your chosen ramp angle.
2
Set "Recoil" to 0 and leave it there for all parts of the lab.
3
Turn on the ruler ruler icon from the Dynamics Track simulation .
4
By trial and error, find an initial speed that will send the cart to approximately the 170-cm point. Record this as your initial velocity, v0. Note that the cart will start at this initial velocity from a dead start when you click Go. Yes, this would be impossible to do with real physical equipment.
5
Calculate and record KE0 in joules for the 0.250-kg cart. (Careful with units!)
6
Turn on the brake and drag the cart so that the cart mast is at approximately the 20-cm point on the ruler.
7
Turn on the Sensor.
8
Quickly click Go to launch the cart. Turn off the Sensor when the cart returns to the bottom.
Note:

You'll need data from the lab apparatus data table later, so don't use the sensor again until you complete Part IA.
9
Record the cart's final velocity and kinetic energy, vf and KEf, respectively, at the top of the cart's travel. (There are no data required for this. Just think about it.)
10
Using conservation of mechanical energy, calculate and record the cart's predicted change in height, Δh = hf – h0.
11
What Δh would you get if you added 0.250 kg to the cart? Try it to make sure of your answer. (No sensor! See the note above.)
12
That doesn't seem right. It appears that there would be no limit to how much mass could be sent through the same Δh. This would have to "cost" us somehow. Where must this extra energy be coming from?
13
Remove the extra 250 grams from the cart.
Experimental Δh from Δx Measurements on the Track and Geometry Let's see how accurate your prediction of Δh is by measuring it.
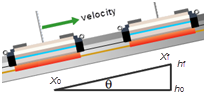
A cart is shown in two positions on a portion of the ramp: its original position lower on the ramp is labeled x 0 and its position higher on the ramp is labeled x f. A arrow points up along the ramp starting from the mast of the lower cart and is labeled velocity. A right triangle is drawn beneath the ramp, with the hypotenuse parallel to the ramp and the right angle in the bottom right. The position x 0 corresponds the bottom left point of the triangle. The position x f is at the other end of the hypotenuse, that point is also labeled h f. The bottom right point of the triagle is labeled h 0.
Figure 4: Δh from Trigonometry
In Figure 4, you see the cart at two positions—original, x0, and final, xf. Of course, these would be reversed if the cart were going down the ramp. You know your ramp angle, θ. And the positions, x0 and xf, can be found in the apparatus data table. You can then find Δh = hf – h0 using
( 7 )
sin(θ) =
Δh
Δx
 =
hf − h0
xf − x0
.
14
Scroll through the position data in the right column of the apparatus data table. The initial and final positions of the cart are x0 and xf, respectively, for the trip up the ramp. How can you find x0 and xf from this data? Be careful—the data includes the motion back down the track, which is not what you're looking for.
15
Record x0 and xf.
16
Calculate and record Δh.
17
Calculate the percentage error in your experimental value of Δh. Use your predicted value as the accepted value.

B. The Relationship Between Speed and Kinetic Energy – Proportional Reasoning

Here's your chance to get a better understanding of the nonlinear relationship between speed and kinetic energy. This is something that gives many students trouble.
1
Question: Suppose you wanted the cart to start at the same x0 point but rise just half as far vertically, that is, ΔhIA/2. That would mean it would have half the value of ΔPE, which would require just half the initial KE since KEf = 0. You selected a v0 that resulted in a particular ΔhIA. What v0 would you use for ΔhIA/2?
2
We'll find it experimentally first. Add three photogates to the apparatus, just for reference markers. (Click the radio button beside "Photo Gates," then reduce "# Gates" to 3.)
3
Put the first gate at 20 cm, the starting point, x0. Put the third one at the xf you found in Part IA (which is also at the original hf(orig)). Do a test run with your original v0 to make sure that the cart rises to the third photogate (approximately) as it should.
4
For your new target, you need to put the middle gate at the point halfway between the first and third gates. That would be at xmid, which would also be at hmid. Also, xmid should be halfway between x0 and the original xf. (Think about it.)
( 8 )
xmid = x0 +
(xf − x0)
2
Calculate and record xmid.
5
You now have a target to shoot at. You first need to experimentally determine the proper v0 to give the cart half of its previous KE. How about v0/2? Try it and see how it works out.
  • a
    How'd that work out? Too fast or too slow?
  • b
    Use trial and error to find your best value for the required initial velocity to just reach xmid. Record v0(mid, expt).
6
Now let's calculate the theoretical initial velocity. Here's the problem and how to think about it.
  • •
    KE0 =
    1
    2
    mv02.
     So KE0 is directly proportional to
    v02,
     not v0. So
    v0
    2
     won't give the cart
    KE0
    2
    .
  • •
    So halving v0 doesn't halve KE0; halving
    v02
     does!
    • •
      If you halve
      v02,
       you will also halve
      1
      2
      mv02.
      1
      2
      m
      v02
      2
  • •
    So if v0(orig) equals your v0 from Part IA, what do
    v0(orig)2, v0(mid)2 =
    v0(orig)2
    2
    ,
     and v0(mid, theo) equal?
7
The proof is in the testing. Give it a try and see if you need further head scratching. (You may need to round to an integer v0.)

II. Work by Friction

As the cart traveled up the ramp in Part IA, gravity did an amount of work equal to –WxΔx on the cart. If the cart is released, on the way back down, gravity would do an amount of work equal to +WxΔx. The total work for the round trip would be zero. That is,
−Wx Δx + (+WxΔx) = 0
 for the round trip. That's the nature of a conservative force. When work is done in moving an object against such a force, an equal amount of work is done by the force when the object is allowed to return to its starting point. It's as if our work is somehow "stored up" until we need it back. Of course, most of the time, mechanical energy is not conserved. As you swim across a pool, the water exerts a backward force against you. If you stop and tread water at the other side of the pool, the water will not return the favor (energy) by pushing you back to where you started! These forces that do a nonzero amount of work when an object is moved around a closed loop are called nonconservative forces. A force like a wind that acts to increase the energy of a sailboat does net positive work. Likewise, a force like friction that removes energy from a system does net negative work. In either case, we can say
( 9 )
Wnc = ΔPE + ΔKE,
where Wnc is the total work done by all nonconservative forces acting. The value of Wnc can be either positive or negative. So it can increase or decrease the energy of an object. In this part of the lab, we'll look at the negative work done by friction. We'll use a level track and observe the decrease in velocity of the cart when friction is acting. Figure 5 shows the set-up. You won't see the vectors while the car is sitting still. (Two figures were merged to create this figure, and the ruler was dragged way up out of the way.) Notice the decreasing velocity to the right and the constant force to the left (Fnet ≡ Ffriction). There is one force acting, and it is friction. Note the boxes with the elapsed time, eT, and the time interval, dT, for the 10-cm-wide purple card to pass through the gate. You'll use dT as explained below.
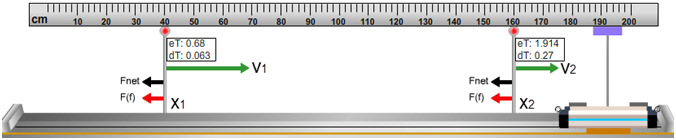
A cart with a friction pad is on the right side of a level track. A ruler is shown over the track. There are two gates indicated one at 160 cm and the other on the left at 40 cm. At 40 cm gate, the net force and force of friction are shown pointing to the left, and the velocity vector is shown pointing to the right. There is also a text box with eT: 0.68 and dT: 0.063. At the 160 cm gate, these same forces with the same magnitude and direction, and the velocity is shorter but still pointing to the right. The text box at this gate has eT: 1.914 and dT: 0.27.
Figure 5: Elapsed Time, eT, and Time Interval, dT
A cart traveling initially at some velocity, v0, at x = 10 cm, slows steadily as it moves from left to right. At x1, it has a velocity, v1. At x2, it has slowed down to v2. It is slowed by a kinetic friction force with some friction coefficient, μk. To find the velocities, v1 and v2, we attach a card of known width to the top of the cart spindle and let it interrupt beams of light (source not shown) shining toward the apparatus. In Figure 6 you see the purple card attached to the top of the cart spindle. The cart, which is moving to the right, is passing in front of the photodetector which repeatedly checks to see if anything blocks the light entering it. A timer is started when the leading edge of the card is at the center of the photogate as shown in Figure 6a. In 6b, the timer stops when the trailing edge of the card is at the center of the gate on the way out.
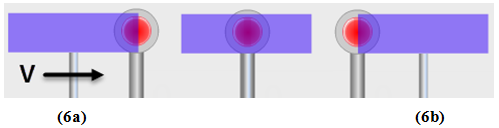
Figure 6: the Measurement of dT
The velocities of the cart at points 1 and 2 can be found using the width of the purple card and the time intervals,
dT1
 and
dT2,
 for the card to pass through a given photogate. These are actually average velocities,
Δx/Δt,
 but the average velocity is approximately equal to the instantaneous velocity at the midpoint.
The work done by friction is given by
Work = ΔKE = KEf – KE0

−FfkΔx =
1
2
m(v22 − v12),
where
Ffk = μkmg

−μkmgΔx =
1
2
m(v22 − v12).
Note that the work is negative since the friction force acts opposite the direction of the motion. The value of
v22 − v12
 is negative as well. Thus, μk will be positive
Your task is to determine the value of μk experimentally and compare it to its known value.
1
Set up two photogates as shown above at x1 = 40 cm and x2 = 160 cm.
2
Set "Card Width" to 10 cm.
3
Position the cart at x = 10 cm and set "V0" to 200 cm/s.
4
Turn on the friction pad and set "μK" to 0.10.
The next three steps are done in succession. It may take a few tries.
5
Click the Take Gate Data button.
6
Click Go.
7
Click the Stop Gate Data button after the cart stops moving.
8
Record your data.
  • Δx: distance between gates, distance traveled while work is done by friction, in m
  • μk: the known kinetic friction coefficient, no units
  • m: the mass of the cart, in kg
  • dT1: time to pass through first gate, in s
  • dT2: time to pass through second gate, in s
  • v1: average speed through first gate (card width/dT), in m/s
  • v2: average speed through second gate, in m/s
Note:

Sometimes the dT values are a bit iffy. You may find that one of the dT values is negative. Also, dT2 should be almost twice dT1. Please try again if you see any suspicious data. And be sure to note that you're recording dT, not eT.
9
Calculate your experimental value for
μk(expt).
10
Calculate the percentage error in your experimental μk(expt). Use the theoretical value as the accepted value.

Copyright © 2013-2014 Advanced Instructional Systems, Inc. and Kentucky Educational Television | Credits