Print

Conservation of Momentum

Purpose

Equipment

  • Virtual Momentum Track
  • VPL Grapher
  • Pencil

Simulation and Tools

Open the Virtual Momentum Track simulation to do this lab. You will need to use the VPL Grapher to complete this lab.

Explore the Apparatus

Open the Virtual Momentum Lab. A lot should look familiar after having worked with the Dynamics Track.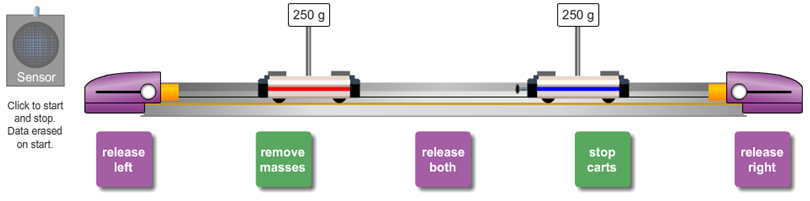
Sensor to the left of a horizontal track. On the track are two carts. Both carts have masts with white flags on the top. The flag for the cart on the left has a red dot and the one for the cart on the right has a blue dot. There are objects at either end of the track. Sticking out from both towards the inside of the track are small cylinders. There is a horizontal groove with a white button in each of the objects. Below the track are the following buttons are radio buttons from left to right: release left - button; Motion Sensor - radio buttons with options Off and On; release both - button; Cart Accessory - radio button with options Spring Plunger and Velcro; release right - button.
Figure 1: Carts, track, and motion sensor in the Virtual Momentum Lab simulation
Let's take a trial run with the apparatus. Toss the carts around a bit to see how they interact. You'll see that they bounce nicely off of each other and lose a bit of speed when they collide with the orange bumpers. Turn on the "Velcro®" and try it again. Hopefully they act as you'd expect. Turn the "Spring Plunger" back on. Start both carts moving. Now click on either cart. The other one stops, too. But when you release the mouse button, the unclicked cart starts moving again. The best way to stop them both is with the Stop Carts button. Try adding some mass to one cart. You have to release the mass while it's over the mast (the rod holding up the flag). Bang the carts around a bit to see how the mismatched carts behave. Now try the launchers. Here's how they're operated: Drag a cart to the launcher bumper and continue dragging it until it appears to go behind the bumper. Release the cart. This engages the cart and bumper. Now cock the launcher spring by pulling back the white circle on the side of the launcher. Click the release button to fire. Try again with the launcher spring pulled back different distances. Try launching both at once (release both). This would be a good time to try out the "Motion Sensor." It's a bit trickier with this lab since you have two carts to work with, as well as abrupt changes in speed and direction. Try this: Double the mass of the red cart by adding 250 grams. Attach it to its launcher and pull back the spring about 50%. Put the blue cart at mid-track. Switch to the "Spring Plunger" if you still have the "Velcro®" on. You'll soon need to change the masses on the carts. You remove masses by double-clicking on the stack of masses. In computer lingo, the order is LIFO. "Last in, first out." The last mass added (the top one) is the first one removed by clicking.
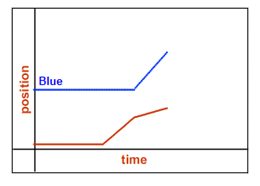
Graph of position versus time. There are two lines drawn on the graph. One is labeled Blue and starts about halfway up the position axis. It is a horizontal line until about half way along the time axis thin it has a steep positive slope. The second line starts just above the origin on the position graph. About a third the way along the time axis it has about a 45 degree positive slope. At the same point on the time axis the the blue line starts have a positive slope, the slope of the second line becomes much shallower.
Figure 2
Let's identify all the parts of this interaction on our graph. When you turn on the "Motion Sensor," each cart is stationary until you click the launcher release button. During this time each cart has an initial, constant position (zero velocity) as indicated by horizontal (t, x) lines.
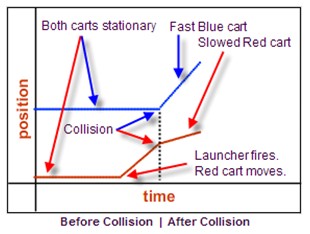
Same as figure 2, however different portions of the graph are labeled. The horizontal lines are labeled: both carts stationary. The point where the second line first starts to have a positive slope is labeled: Launcher fires, red cart moves. There is a vertical dashed line connecting the point where the blue line starts to have a positive slope and the second line starts to have a shallower slope and on down to the origin. This is labeled as the collision. Below the graph and to the left of this vertical line is labeled before collision and below the graph and to the right of this line is labeled after collision. The positive slope of the blue line is labeled fast blue cart. The shallower slope for the second line is labeled slowed red cart..
Figure 3
When the launcher is fired, the red cart is given an initial velocity. (We ignore acceleration in these graphs.) The red cart collides with the blue cart. The red cart is pushed to the left, slowing it down. The blue cart is pushed to the right with an equal but opposite force, thus giving it a positive velocity which appears to be somewhat faster than the red cart's initial velocity. Let's analyze our data. You have five velocities, but you're interested in only four of them. You are only interested in the velocities just before and just after interactions—collisions. The blue cart is at rest before, and traveling at some positive velocity after the collision. The red cart has a positive velocity before and a smaller positive velocity after the collision. The red cart's initial zero velocity before launch is not related to the collision. You'll always ignore similar segments. The blue cart's initial zero velocity is obvious from the graph. Let's see how to find the other velocities using Grapher.
1
In the momentum apparatus, click Copy Data to Clipboard.
2
Open Grapher. Click in the "paste data" box and use Ctrl+V to paste it into the data table.
3
You should see three columns of data labeled "X," "Blue," and "Red." These hold the data for time, blue cart position, and red cart position, respectively. You should also see two graphs—one position-time graph for each cart. Use manual scaling to make sure that each graph starts at (0, 0) and has the same maximum x and t values. A range of 0.0 m to 2.0 m is good. Label the axes of the top graph "Blue Position (m)" and "Time (s)." Label the bottom graph similarly. Give each graph an appropriate name.
4
Turn on "Linear Fit." Determine the constant velocities of the carts prior to the collision by finding the four slopes of their (t, x) graphs. You should know how to use the "Linear Fit" tool from your kinematics labs or by studying the Lab Guide. You'll note that when you drag across a certain portion of the graph, a pink line of best fit is drawn for that range of points. The data in the "Linear Fit" data box also corresponds to that data range. Thus you can determine before-and-after-collision velocities for each cart. The longer the line segment you drag across, the better your results will be.
You should now have something like Figure 4. (Actually, Figure 4 has been cobbled together from both graphs to make it easier to compare the graphs.) The actual velocity values depend on your initial plunger setting.
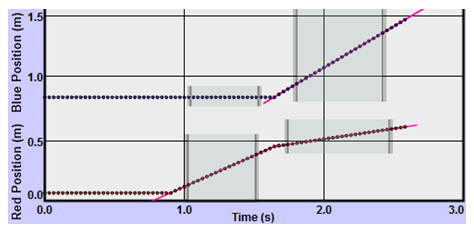
2 plots with the y axis is labeled Red Position (m) on the bottom portion and Blue Position (m) on the upper portion. The scale goes from 0.0 to 1.5. The x axis is labeled Time (s) and has a scale from 0.0 to 3.0. The graph in the Red Position portion is a series of closely spaced points that starts at the origin and is a horizontal line until about 0.9 s when it has a positive slope. At around 1.7 s the slope becomes shallower. A region of the first positive slope is highlighted and a pink straight line passes through these points. A region of the shallower positive slope is highlighted and has a straight pink line. The graph next to Blue Position is also a series of closely spaced points. It starts at about (0.0, 0.8) and is horizontal until about 1.7 s when the line has a positive slope that is steeper than the other slopes. A section of the horizontal line is highlighted. A portion of the line with the positive slope is highlighted and a straight pink line passing through those points.
Figure 4
The slopes produced by Grapher are as follows.
Vo Blue = 0 m/s
Vo Red = 0.517 m/s
Vf Blue = 0.686 m/s
Vf Red = 0.174 m/s
These velocities and the masses are the only values needed to analyze the momenta and energies of our carts.

Theory

Momentum

In class and in your reading, you've seen the following development of the concepts of momentum, momentum conservation, and their connection to energy conservation. (Vectors are shown in bold type.) The momentum, p, of a body of mass, m, and velocity, v, is written as
( 1 )
p = mv.

Case 1: A net external force acts on a body.

When a (net) force acts on a body, its velocity and hence its momentum will change according to equation 2.
( 2 )
FΔt = Δp
where FΔt is referred to as the impulse, J. Note that the impulse is a vector and is equal to the difference in two momentum vectors, pf and po. In words, equation 2 says
( 3 )
impulse = change in the momentum.

Case 2: An internal force acts between two bodies (or more than two, but that's out of our league).

As you know, forces come in equal and opposite pairs. So you know that in case 1 you were just focusing on one of the bodies involved. That's great for determining things like the effect of the force on a golf ball hit by a golf club. There are also many situations where it's useful to look at both bodies involved. If you want to slow down or change the course of an incoming asteroid, you need to know how big an object you need to throw at it, how fast you need to throw it, and in what direction. In these cases, the impulse on the system is zero since all forces are internal to the system. When there is a no net, external force,
( 4 )
FΔt = Δp = 0.
That is, there is no impulse, so there will be no change in momentum. Thus the momentum of the system is conserved.
( 5 )
p(sys)o = p(sys)f
So, if there is no net, external force on the system, the momentum of the system will remain unchanged even if the parts of the system exert forces on one another and the individual parts change their momentum.
An excellent example of this behavior is the system of two carts that you collided together earlier. Their total momentum before the collision, po, was equal to their total momentum after the collision, pf. Try using the data in Figure 4 to verify the following. For a system of two carts, you can expand p(sys)o = p(sys)f to
( 6 )
p1o + p2o = p1f + p2f.
After rearranging,
( 7 )
Δp1 = −Δp2.
That is, the loss in momentum by cart one equals the negative of the gain in momentum of cart two.

Kinetic Energy

You've also become familiar with the kinetic energy, KE, of an object. The equation for kinetic energy involves the same terms, m and v.
( 8 )
KE =
1
2
mv2
So, shouldn't the kinetic energy of the system always be conserved, too? That is, shouldn't it be the same before and after an interaction? No. There's a subtle difference between the equation mv for momentum and
1
2
mv2
 for kinetic energy. The v in kinetic energy is just the speed, a scalar. So, kinetic energy is a positive scalar, and we could never add up two kinetic energies for a result of zero. Kinetic energy is not necessarily conserved. Momentum is always conserved. In this lab, we'll observe the momentum of a system of two carts in several situations. We'll also investigate their kinetic energies.

Procedure

Please print the worksheet for this lab. You will need this sheet to record your data.

PDF file

I. Conservation of Momentum in a Collision

Note:

In most of this lab, you'll use your data to answer questions, even non-numerical questions.
Equations 6p1o + p2o = p1f + p2f. and 7
Δp1 = −Δp2.
 say the same thing, but in two different ways. Let's explore both.
1
Load the blue cart with 500 g, giving it a total mass of 750 g. (Remove any mass that has been added to the red cart.)
2
Position the blue cart right between the release both and stop carts buttons.
3
Engage the red cart with its launcher. Cock the launch spring about halfway back.
4
Turn on the "Motion Sensor."
5
Release the left cart.
6
Somewhat before the blue cart hits the right bumper, turn off the "Motion Sensor." Your graph should look something like Figure 5.
There may be additional lines due to collisions with the plungers. Ignore them. Dragging the big white ball below the graph will adjust the time display scale.
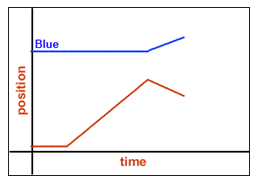
Graph of position versus time. There are two lines drawn on the graph. One is labeled Blue and starts about halfway up the position axis. It is a horizontal line until about half way along the time axis thin it has a shallow positive slope. The second line starts just above the origin on the position graph. About a quarter the way along the time axis it has about a 45 degree positive slope. At the same point on the time axis the the blue line starts have a positive slope, the slope of the second line becomes negative and shallower.
Figure 5
Before finding actual values for the velocities, let's think about what the graph tells us about the signs of the momenta.
7
What is the sign of the red cart's initial momentum, mRvRo, its momentum just before the collision?
8
What is the sign of the red cart's final momentum, mRvRf, its momentum just after the collision?
9
What is the sign of the change in the red cart's momentum, Δ(mRvR) = mR(ΔvR)?
10
The blue cart's initial momentum, mBvBo, doesn't have a sign. What is its momentum before the collision?
11
What is the sign of the blue cart's final momentum, mBvBf, its momentum just after the collision?
12
What is the sign of the change in the blue cart's momentum, Δ(mBvB) = mB(ΔvB)?
So the red cart had a negative change in momentum while the blue cart had a positive change in momentum. If the total momentum must be constant, then the sum of these changes, the total change, must add to zero. Let's look at the numbers.
13
Copy+Paste your data from the apparatus into Grapher as before. Using the "Linear Fit" tool, determine the carts' velocities before (Vo) and after (Vf) the collision. Record these in Table 1.
14
Using the known masses calculate and record the momentum of each cart before and after the collision (4 values).
15
Add the initial momenta of the carts to determine the initial momentum (p(sys)o) of the system. Similarly determine the final momentum (p(sys)f) of the system. Record these two values in Table 1.
16
Finally, calculate and record the change in momentum of the system (Δpsys) from (p(sys)f) – (p(sys)o).
17
Equation 6p1o + p2o = p1f + p2f. says that p(red)o + p(blue)o = p(red)f + p(blue)f. How did that work out? Quote your numbers.
18
Equation 7
Δp1 = −Δp2.
 says that p(red)f – p(red)o = –(p(blue)f – p(blue)o). How did that work out? Quote your numbers.

II. Elastic Collisions

With the "Spring Plunger," the carts seemed to bounce nicely off of each other. Could this have been an elastic collision, that is, one where the kinetic energy of the system was unchanged during the collision? Let's do the math and see.
1
Table 2 works just like Table 1 and uses the same data. By filling in Table 2, you'll calculate the total KE of the system of two carts before (KE(sys)o) and after (KE(sys)f) the collision. You'll also calculate the change in kinetic energy of the system, ΔKEsystem, which is KE(sys)f – KE(sys)o. Note that in the equation for KE, only the speed is considered. That is, KE has no direction associated with it. This actually doesn't matter in your calculations since all the velocities are squared.
2
Does the kinetic energy of the system appear to be conserved in this collision? How do you know? Quote your numbers.

III. Totally Inelastic Collisions

In the previous section, we observed carts making elastic collisions. We found that both momentum and kinetic energy were conserved. Our carts can have another type of collision. The springy bumpers between them can be replaced by sticky "Velcro®" bumpers. In this case we would have a totally inelastic collision, one where the carts stick together after the collision and share a common speed.
1
Let's start with the simplest case – a collision between carts of equal mass and equal but opposite velocities. Attach both carts to their launchers. Remove all extra masses. Fully cock both launchers (to provide equal initial speeds). Using the usual procedure, produce a graph of their head-on collision. You'll need to use the release both button.
  • a
    Copy and paste your data into Grapher. Add axis labels and an appropriate title to each graph. Manually adjust the y-axis scale on both graphs to range from 0.0 m to 2.0 m.
  • b
    Take a single Screenshot screenshot icon from Grapher of the graph from Grapher and upload it as "Mom_III1.png".
  • c
    Draw the position-time graph produced by the apparatus in Graph III1.
  • d
    Explain how you know from the graph(s) that momentum was conserved, but kinetic energy was not. You should be able to tell just by looking at the graphs, but you can use Grapher to assist you.
Empty coordinate axes with the x axis labeled Time (s) and the y axis labeled Position (m).
Figure Graph III1: Head on Equal speed collision
2
Now try a similar collision, but this time with the blue cart initially sitting still at the center of the track.
  • a
    Copy and paste your data into Grapher. Again manually adjust the y-axis scale on both graphs to range from 0.0 m to 2.0 m. Add axis labels and an appropriate title to each graph.
  • b
    Take a single Screenshot of the pair of graphs from Grapher and upload it as "Mom_III2.png".
  • c
    Draw the position-time graph produced by the apparatus in Graph III2.
  • d
    This one's not so obvious. You'll need some data and calculations to work with. Use Grapher to get the data you need. Use Table 3 to record your data and calculated values.
Empty coordinate axes with the x axis labeled Time (s) and the y axis labeled Position (m).
Figure Graph III2: Collision with stationary cart
3
Using your data, explain how you know that momentum was conserved, but kinetic energy was not conserved.
4
You should have found that the pair of carts moving as one with a mass of 2 × mcart had half the speed of the single cart with a mass of 1 × mcart. Why then is the kinetic energy less after the collision? That is, why doesn't one cart with a speed of v have the same kinetic energy as two carts each with a speed of
v
2
?
 (Here's a head start to your answer: Before the collision, the object carrying all the momentum and KE had a mass of mcart and a speed of Vo.)
5
For the situation in Graph III1, what fraction of the kinetic energy of the carts remains after the collision? That is, what is (KEfinal/KEinitial)? You don't have any numbers to work with, but you don't need any.
6
For the situation in Graph III2, what fraction of the kinetic energy of the carts remains after the collision? That is, compute (KEfinal/KEinitial). You'll need to use your numbers this time.

Copyright © 2013-2014 Advanced Instructional Systems, Inc. and Kentucky Educational Television | Credits