Archimedes' Principle
Purpose
-
•To connect the words of Archimedes' Principle to the actual behavior of submerged objects.
-
•To examine the cause of buoyancy; that is, the variation of pressure with depth in a fluid.
-
•To use Archimedes' Principle to determine the density of an unknown material.
Equipment
- Virtual Buoyancy Apparatus
- Pencil
Simulation and Tools
Open the Buoyancy Apparatus simulation to do this lab.Explore the Apparatus
We'll use the Buoyancy Apparatus in this lab activity. You can get quick access to help by rolling your mouse over most objects on the screen.
Figure 1: The Buoyancy Apparatus
Archimedes' Principle:
A body wholly or partially immersed in a fluid will experience a buoyant force equal to the weight of the fluid displaced.
A body wholly or partially immersed in a fluid will experience a buoyant force equal to the weight of the fluid displaced.
1. What's a "Buoyant Force", and What Exerts it?
Let's try it with the system in Figure 1. Right (or Ctrl) click and zoom in on the hanging scale. It appears to read zero initially. This sort of scale is not very precise. Our simulation reflects that level of precision. (Zoom back out.) Now drag the cork and aluminum compound object and drop it somewhere below the hanger. It should become attached to the hanger. (If it refuses to attach, you probably have the scale already lowered somewhat, or there might be some water in the graduated cylinder.) You should find that it weighs about 4.4 N. Zooming in and estimating a digit we might have 4.41 N. Drag and drop it on the digital scale and you'll get a more precise answer of about 4.41 N. Which scale should you use? We'll always use the value from the hanging scale, 4.41 N in this case, unless we have to use the digital scale for a measurement. This will only happen when we need to weigh the graduated cylinder. Now for the "(submerged) weight when fully or partially immersed in the water." Drag the object back to the hanging scale. Slowly drag the support arm above the scale downward until the aluminum disk is about half submerged. The scale might read about 3.73 N. This is a judgment call since the location of the half-way point is uncertain. Let's use that value in the following discussion. That's the "submerged weight." We'll use the termW'
("W prime") to represent the submerged weight.
So, its actual weight is 4.41 N and it appears lighter when partially submerged, maybe 3.73 N. It didn't lose weight. The water is providing an upward force on the bottom of the disk. So, we would say that a 4.41-N object was buoyed up by a force Fb so that it appears to weigh, or has a submerged weight of, 3.73 N. Since it's in vertical equilibrium, we can say | F | |
 | |
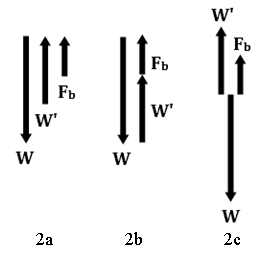
Figure 2
| = | Weightsubmerged + Fb + Weight = 0 | ||||
| = | W′ + Fb + W = 0 |
W' + Fb − W = 0,
Fb = W − W ′.
a
Fb = W − W ′ = 4.41 N − 3.73 N = N.
2. What is the "Fluid Displaced" and How is its Weight Related to the Buoyant Force?
In the preceding section, you focused on the buoyant force as an apparent reduction in the weight of the submerged object. What's the source of this force? With the cork and aluminum disk pair attached to the scale, lower the scale as far as it will go. A lot of water will overflow into the cylinder. When that's done, raise the scale back up. Now gradually lower the disks into the water. Notice the behavior of the water. Its level rises because the disks are "displacing" some of the water. That is, they're taking the water's place. So it rises to make room. When the water occupied that space, it was supported by the water below it. When the disks occupy the same space, the water below them provides exactly the same amount of upward force. That's the buoyant force. It was there all the time, but it was just holding up the water until the disks arrived. So "the buoyant force is equal to the weight of the fluid displaced!" We need to find out how to determine that weight. Refill the tank. To do this just drag the graduated cylinder somewhere above the tank and release it. It will empty itself and return to its post. Now gradually lower the disks into the water and notice what happens to the "displaced water." Since our tank was initially full this time, the displaced water overflowed into the graduated cylinder. We did that so that we could weigh it or find its volume. Let's use our previous results to see the relationship between the buoyant force and the displaced fluid's weight. If your apparatus is not right where you left it at the end of Part 1, repeat Part 1 to restore it. Be sure to zoom in once for better precision. Insert your value from 1a in the following blank.b
The displaced water's weight = the buoyant force on the disk = N
c
Drag the graduated cylinder onto the digital scale. Scale reading with cylinder and water = N
d
Weight of empty graduated cylinder, Wc = N
e
Fb = weight of water displaced = Wwater + cylinder – Wcylinder = N
Ex: (1.69 – 0.98)N = 0.71 N
3. Finding and Using the Volume of the Fluid Displaced
Now suppose we didn't have either of our scales. Could you still determine Fb? We know that the weight of the water can be found from Wwater = mwaterg = ρwatergVwater. Since we know that the density of water is 1000 kg/m3, we could calculate the weight of the water if we knew its volume. You can zoom in on the cylinder to read the volume reading, but there's a "Cylinder Zoom" feature that does that for you. You can now read the volume in mL.Note:
The graduated cylinder measures volume in mL. You'll always need to convert it to m3. (1 mL = 1 cm3 = 10–6 m3)
The graduated cylinder measures volume in mL. You'll always need to convert it to m3. (1 mL = 1 cm3 = 10–6 m3)
f
Use the equation below to find Fb.
Fb = Wwater displaced = ρwatergVwater = 1000 kg/m3 × 9.80 N/kg × m3 = N
Ex:
How about the aluminum disk? If you weighed it and then completely submerged it, you could measure its volume and then compute its density and convince the king that his disk is not silver.
Incidentally, we went to extra expense in providing a non-wetting polypropylene graduated cylinder in this apparatus to avoid the need to account for a meniscus. You're welcome.
1000 kg/m3 × 9.80 N/kg × 72 × 10−6 m3 = 0.71 N
Theory
Archimedes' Principle
Archimedes' Principle is very easy to state in words, but learning how to use it takes practice in a variety of situations. In this lab, we'll first explore the literal meaning of this principle. Then we'll put it to use in a couple of situations. You'll use the wording of the principle to draw free-body diagrams (FBDs) and create equations that can be used to find unknown quantities such as the volume, mass, or density of an object or of the fluid it's immersed in. Solving problems using Archimedes' Principle can be really puzzling. The most important step is to use the words of the principle to create an equation. One important tool to help you create your equation is a free-body diagram. Archimedes' Principle usually involves objects in vertical equilibrium. And the terms that go into| F | |
 | |
Archimedes' Principle:
A body wholly or partially immersed in a fluid will experience a buoyant force equal to the weight of the fluid displaced.
A body wholly or partially immersed in a fluid will experience a buoyant force equal to the weight of the fluid displaced.
Variation of Pressure with Depth
Click the Pressure button to load an interactive simulation. Adjust the small cylinder up and down as needed to recreate the discussion that follows. In Figure 3a, a solid brass cylinder is shown above a tank completely filled with water. Atmospheric pressure acts essentially equally on all sides of the cylinder and on the water's surface as indicated by the five Patm arrows in Figure 3a. At all times the horizontal pressures will cancel. So we need only examine the vertical pressures.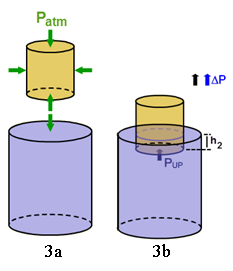
Figure 3
1
What happens to the upward pressure, Pup, and ΔP as the cylinder is lowered? Don't let the cylinder become completely submerged for now.
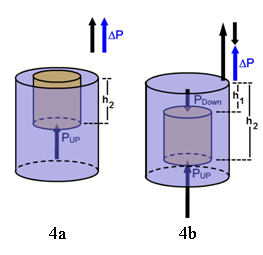
Figure 4
2
Where is the top of the cylinder when this transition occurs?
3
What happens to ΔP as the cylinder is lowered while completely submerged?
4
What happens to Pup and Pdown as the cylinder is lowered while completely submerged? How does this account for your answer to the previous question?
P2 − P1 = ρg(h2 − h1).
In the case of a partially submerged object, h1 = 0,
so this equation will work for either a partially or fully submerged object.
The Effect of the Pressure Difference, ΔP, on the Buoyant Force
We've found a simple equation that gives the pressure difference between the top and bottom of our cylinder when it's somewhat or totally submerged. So how does this relate to buoyancy?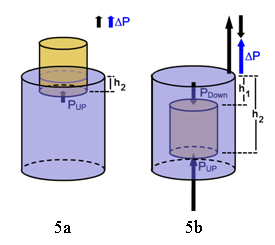
Figure 5: Note that 5a is the same as 3b, and 5b is the same as 4b.
Fnet water = F2 − F1 = (P2 − P1)Ac = ρg(h2 − h1)Ac.
h2 =
hc,
| 1 |
| 4 |
ρwg(h2 − h1)
reduces to ρwg
hc
.
The total force, Fnet water, exerted by the water pressure on the cylinder would be
 |
| 1 |
| 4 |
 |
| Fnet water | = | ρwg
| ||||
| = |
| |||||
| = | the weight of the water that would occupy
| |||||
| F2 | = | "the weight of the water displaced." |
h2 − h1 = hc
, so ρwg(h2 − h1)
reduces to ρwghc
.
The total force, Fnet water, exerted by the water pressure on the cylinder would be
| Fnet water | = | ρwghcAc |
| = | ρwgVc | |
| = | the weight of the water that would occupy the total volume of the cylinder | |
| F2 | = | "the weight of the water displaced." |
So, no matter what volume of the cylinder is submerged, the buoyant force acting on it equals the weight of an equal volume of water.
5
As a cylinder of aluminum is lowered into our tank, when will the buoyant force, Fb, begin to exceed the cylinder's weight?
(a) when it's partially submerged; (b) when it's fully submerged; (c) never
6
Why is this the case?
7
Once the cylinder of aluminum is fully submerged, we might hold it in place by attaching which of the following?
(a) a block of cork; (b) a block of aluminum; (c) a block of water; (d) none necessary
8
As a cylinder of water is lowered into our tank, when will the buoyant force, Fb, begin to exceed the cylinder's weight?
(a) when it's partially submerged; (b) when it's fully submerged; (c) never
9
Why is this is the case?
10
Once the cylinder of water is fully submerged, we might hold it in place by attaching which of the following?
(a) a block of cork; (b) a block of aluminum; (c) a block of water; (d) none necessary
11
As a cylinder of cork is lowered into our tank, when will the buoyant force, Fb, begin to exceed the cylinder's weight?
(a) when it's partially submerged; (b) when it's fully submerged; (c) never
12
Why is this is the case?
13
Once the cylinder of cork is fully submerged, we might hold it in place by attaching which of the following?
(a) a block of cork; (b) a block of aluminum; (c) a block of water; (d) none necessary
14
It's useful to leave all three cylinders fully submerged at about the same depth and then click the different icons to switch among the three materials. There is one thing that is the same regardless of the cylinder chosen. What is it? Why?
Archimedes' Principle with Additional Applied Forces
Most of our work with Archimedes' Principle includes additional forces such as the ones suggested at the end of each of the three sets of questions above. Typical examples include:-
•A lifeguard pulling a person up onto a dock will find that the person seems to get heavier as she's lifted further out of the water. This leads to the strategy of starting out with a large upward pull to give the swimmer an initial upward speed, making the rest of the pull easier.
-
•A buoy in a river will be held in place by a heavy weight sitting on the river bottom. The "one final question" above will come into play in this case.
-
•The buoyant force might be used to partially or fully support another object. For example, a life jacket has to supply enough buoyant force to support its own weight as well as the person wearing it. A waterlogged life jacket might continue to supply the same lift, but the added water will provide an additional undesirable downward force.
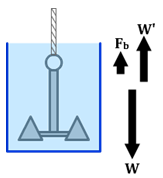
Figure 6
Fb + W ′ = W.
Other considerations:
| Fb | = | weight of fluid (water) displaced |
| = | ρwatergVwater = ρwatergVanchor, |
Procedure
Please print the worksheet for this lab. You will need this sheet to record your data. In the following sections, you'll collect and analyze data to investigate Archimedes' Principle in some typical situations, such as the one suggested in Example 1. You won't be provided step-by-step directions, but you'll have blanks provided for the data you need to collect. This method is being used because buoyancy problems are always sort of free-form. It's not about finding an equation that fits; rather, you'll try to find a way that your information fits into Archimedes' Principle. You'll also get guidance in developing FBDs as well as equations describing your FBDs. Note that the equations are in scalar form. That is, we'll say "The sum of the upward forces = the sum of the downward forces" (all positive magnitudes) rather than "The sum of the upward forces + the sum of the downward forces = 0" (all vectors).I. Confirm Archimedes' Principle for the Case Where ρobject > ρliquid Using Overflow
In this section, we'll directly measure the buoyant force and the weight of the water displaced for an object that sinks. We'll then confirm that they are equal. Our object will be an aluminum disk. If either the Buoyancy or Pressure simulation is still open, click the Close button.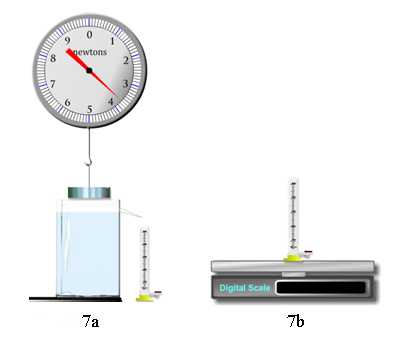
Figure 7a and Figure 7b
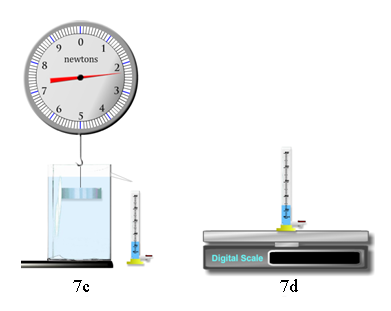
Figure 7c and Figure 7d
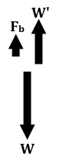
FBD 7e
Fb + Wal' = Wal,
1
Collect and record the following data: Wal, Wcyl, Wal′, Wcylw.
2
Calculate the buoyant force, Fb, twice, using equation 2 and equation 3.
Show your calculations of Fb for each method and the percentage difference between the two.
II. Confirm Archimedes' Principle for ρobject < ρliquid Using Overflow
In this section, we'll directly measure the buoyant force and the weight of the water displaced for a floating object, and we'll confirm that they are again equal. Our object will be a cork disk. This time, you'll fill in all the missing pieces. Use Part I as a model. Collect and record the data required below.
Also fill in the missing pieces below, including Figures 8a, 8c, 8d, and FBD 8e.
1
Submit your responses for Figures 8a, 8c, and 8d by uploading Screenshots
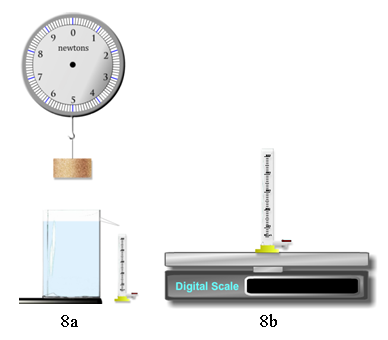
Figure 8a and Figure 8b

Figure 8c and Figure 8d
2
Weighing the cork disk in air (Figure 8a) gives us Wcork. Weighing it when partially submerged (8c) gives us Wcork'. This time it floats. (Note the slack string.)
So, Wcork' = N.
3
Draw FBD 8e to the left of the floating cork provided. There should be two force vectors. Also use the Sketch tool

FBD 8e
Fb = Wal − Wal'.
and 3Fb = Wwater displaced = (Wcylw displaced) − Wcyl
as a guide in producing equations 4 and 5.
4
From FBD 8e, we can say that
Weighing the empty graduated cylinder (8b) gives us Wcyl. Weighing the cylinder after receiving the overflow water (8d) gives us Wcylw displaced.
5–8
Collect and record the following data: Wcork, Wcyl, Wcork′, Wcylw.
9–11
Calculate the buoyant force, Fb, twice, using equation 4 and equation 5.
Show your calculations of Fb for each method and the percentage difference.
III. Determine the Density of an Unknown Material
We've confirmed that Archimedes' Principle correctly describes the forces acting on a body wholly or partially submerged. That gives us a starting point for more complex situations that are not so straightforward. One of your object choices is a compound object with a cork on top and a rod of negligible volume connecting it to a large black unknown object below it. It's in the right-hand column. The unknown object is more dense than cork; otherwise, the system would try to flip upside down. Your task is to determine the density of the unknown object. In the process, you'll first have to determine the density of the cork.Density of the Cork
You already know the weight of the cork from Part II. From the weight, you can calculate the mass. What you need is the cork's volume. You can find that using another compound object–the cork with the attached aluminum disk. It's in the middle of the left column of objects.1–7
Attach the cork/aluminum object to the hanging scale. Lower the system slowly while watching the water overflow into the cylinder. Continue until the aluminum cylinder becomes completely submerged. Use "Cylinder Zoom" to read and record the volume of water displaced by the aluminum.
Continue a bit further to see that the connecting rod is ignored, causing no overflow. Continue on and notice that the cork becomes completely submerged. You want to know the volume of the cork. Record the following data to find the volume of the cork, convert it to m3, and compute its density in kg/m3.
1
Val in ml
2
Val + cork in mL
3
Vcork in mL
4
Vcork in m3
5
Wcork in N (from Part II)
6
Mcork in kg
7
ρcork in kg/m3
Finding the Density of the Unknown Material
Return the cork/aluminum object to its home. Empty the graduated cylinder.8
Attach unknown system #2 (bottom left) to the hanging scale. Gradually lower it as far down as it will go. What is different about this compound system relative to the cork/aluminum system?
9
Draw FBD 9 to the left of the floating cork-unknown system provided. Also use the Sketch tool to create a screen-sketch by adding and labeling vector arrows to the left of the floating cork in the Buoyancy Apparatus. Take a Screenshot of the FBD and the cork and upload it as "Buoy_FBD9.png".

FBD 9
11
We want to know the density of the unknown material, ρu. If we could find its weight, we could use Wu = ρugVu,
since we know g and we can measure Vu using our overflow system.
So to find ρu, we just need Wu. We know Wcork, so if we knew Fb, we could find ρu using equation 6.
From equations 4 and 5, you know two different ways of finding Fb. So you're ready to go.
So we have two equations, Fb = Wcork + Wu,
and Wu = ρugVu.
Combine the two equations and solve for ρu. Show your algebra.
12–16
Determine the total buoyant force, Fb, by either of the methods suggested above.
Show your calculations of the buoyant force, Fb, and the unknown density, ρu.
17
The unknown material is concrete. Check online to see if your result is reasonable. Note that concrete varies in density depending on its manufacture.

