Print

Simple Harmonic Motion – Concepts

Introduction

Have you ever wondered why a grandfather clock keeps accurate time? The motion of the pendulum is a particular kind of repetitive or periodic motion called simple harmonic motion, or SHM. The position of the oscillating object varies sinusoidally with time. Many objects oscillate back and forth. The motion of a child on a swing can be approximated to be sinusoidal and can therefore be considered as simple harmonic motion. Some complicated motions like turbulent water waves are not considered simple harmonic motion. When an object is in simple harmonic motion, the rate at which it oscillates back and forth as well as its position with respect to time can be easily determined. In this lab, you will analyze a simple pendulum and a spring-mass system, both of which exhibit simple harmonic motion.

Discussion of Principles

A particle that vibrates vertically in simple harmonic motion moves up and down between two extremes y = ±A. The maximum displacement A is called the amplitude. This motion is shown graphically in the position-versus-time plot in Figure 1.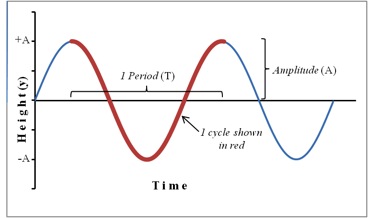
Plot of height in y-axis and time in x-axis showing line motion rising towards +A and then following towards -A below x-axis. One period (t) is a full wave from +A to -A and then back to +A. The amplitude (A) is the the space between the x-axis and +A or -A.
Figure 1: Position plot showing sinusoidal motion of an object in SHM
One complete oscillation or cycle or vibration is the motion from, for example,
y = −A
 to
y = +A
 and back again to
y = −A.
 The time interval T required to complete one oscillation is called the period. A related quantity is the frequency f, which is the number of vibrations the system makes per unit of time. The frequency is the reciprocal of the period and is measured in units of Hertz, abbreviated Hz;
1 Hz = 1 s−1.
( 1 )
f = 1/T
If a particle is oscillating along the y-axis, its location on the y-axis at any given instant of time t, measured from the start of the oscillation is given by the equation
( 2 )
y = A sin(2πft).
Recall that the velocity of the object is the first derivative and the acceleration the second derivative of the displacement function with respect to time. The velocity v and the acceleration a of the particle at time t are given by the following.
( 3 )
v = 2πfA cos(2πft)
( 4 )
a = −(2πf)2[A sin(2πft)]
Notice that the velocity and acceleration are also sinusoidal. However, the velocity function has a 90° or π/2 phase difference while the acceleration function has a 180° or π phase difference relative to the displacement function. For example, when the displacement is positive maximum, the velocity is zero and the acceleration is negative maximum. Substituting from equation 2 into equation 4 yields
( 5 )
a = −4π2f2y.
From equation 5, we see that the acceleration of an object in SHM is proportional to the displacement and opposite in sign. This is a basic property of any object undergoing simple harmonic motion. Consider several critical points in a cycle as in the case of a spring-mass system in oscillation. A spring-mass system consists of a mass attached to the end of a spring that is suspended from a stand. The mass is pulled down by a small amount and released to make the spring and mass oscillate in the vertical plane. Figure 2 shows five critical points as the mass on a spring goes through a complete cycle. The equilibrium position for a spring-mass system is the position of the mass when the spring is neither stretched nor compressed.
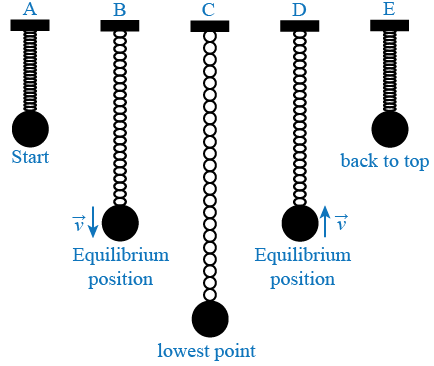
A spring oscillation in five steps, A, B, C, D, and E. A is the start, B shows equilibrium position with arrow pointing down, and V pointing to the right. C shows lowest point of the spring. D shows equilibrium position arrow pointing up, and V pointing to the right. E shows the spring back to the top.
Figure 2: Five key points of a mass oscillating on a spring
The mass completes an entire cycle as it goes from position A to position E. A description of each position is as follows.
Position A: The spring is compressed; the mass is above the equilibrium point at
y = A
 and is about to be released. Position B: The mass is in downward motion as it passes through the equilibrium point. Position C: The mass is momentarily at rest at the lowest point before starting on its upward motion. Position D: The mass is in upward motion as it passes through the equilibrium point. Position E: The mass is momentarily at rest at the highest point before starting back down again.
By noting the time when the negative maximum, positive maximum, and zero values occur for the oscillating object's position, velocity and acceleration, you can graph the sine (or cosine) function. This is done for the case of the oscillating spring-mass system in the table below and the three functions are shown in Figure 3. Note that the positive direction is typically chosen to be the direction that the spring is stretched. Therefore, the positive direction in this case is down and the initial position A in Figure 2 is actually a negative value. The most difficult parameter to analyze is the acceleration. It helps to use Newton's second law, which tells us that a negative maximum acceleration occurs when the net force is negative maximum, a positive maximum acceleration occurs when the net force is positive maximum and the acceleration is zero when the net force is zero.
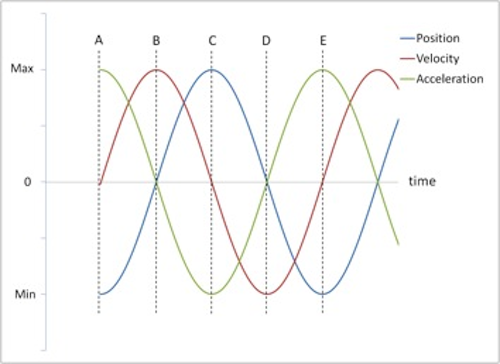
Plot of position, velocity, and acceleration as waves, versus time as the x-axis. The top of the plot is labeled with max, and the bottom is labeled with min. A, B, C, D, and E are labeled by dotted lines, in order, intersecting the x-axis. Position line begins at min on A, reaches max at C, and then min again At E. Velocity line begins at 0, or x-axis, reaches max at B, min at D, and max again after E. Acceleration line begins at max on A, reaches min at C, and max again at E.
Figure 3: Position, velocity and acceleration vs. time
For this particular initial condition (starting position at A in Figure 2), the position curve is a cosine function (actually a negative cosine function), the velocity curve is a sine function, and the acceleration curve is just the negative of the position curve.

Mass and Spring

A mass suspended at the end of a spring will stretch the spring by some distance y. The force with which the spring pulls upward on the mass is given by Hooke's law
( 6 )
F = −ky
where k is the spring constant and y is the stretch in the spring when a force F is applied to the spring. The spring constant k is a measure of the stiffness of the spring. The spring constant can be determined experimentally by allowing the mass to hang motionless on the spring and then adding additional mass and recording the additional spring stretch as shown below. In Figure 4a, the weight hanger is suspended from the end of the spring. In Figure 4b, an additional mass has been added to the hanger and the spring is now extended by an amount
Δy.
 This experimental set-up is also shown in the photograph of the apparatus in Figure 5.
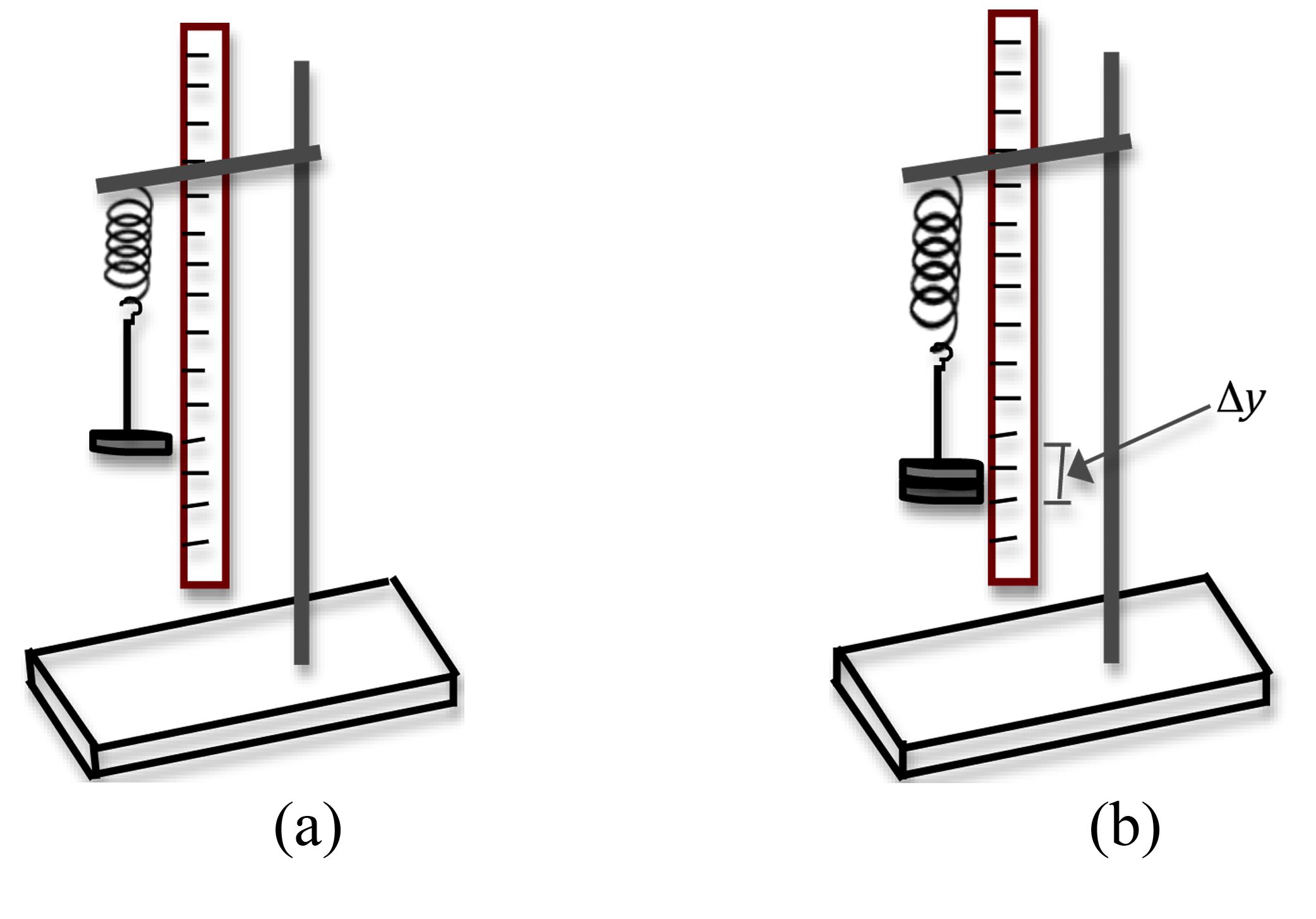
4a is diagram image of weight hanger on spring suspended from stand next to ruler. 4b is image weight placed in weight hanger, displaying an extra extension of delta-y.
Figure 4: Set up for determining spring constant
4a is a photograph showimg image of weight on spring suspended from stand next to ruler. 4b shows additional weight added to the spring.
Figure 5: Photo of experimental set-up
When the mass is motionless, its acceleration is zero. According to Newton's second law, the net force must therefore be zero. There are two forces acting on the mass: the downward gravitational force and the upward spring force. See the free-body diagram in Figure 6 below.
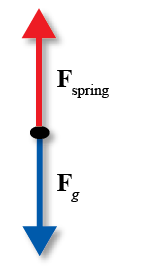
Red vector arrow labeled f sub spring pointing upward from point, and blue vector arrow labeled F sub g point down.
Figure 6: Free-body diagram for the spring-mass system
So Newton's second law gives us
( 7 )
Δmg − kΔy = 0
where
Δm
 is the change in mass and
Δy
 is the change in the stretch of the spring caused by the change in mass, g is the gravitational acceleration, and k is the spring constant. Equation 7 can also be expressed as
( 8 )
Δm =
k
g
 Δy.
Newton's second law applied to this system is
ma = F = −ky.
 Substitute from equation 5
a = −4π2f2y.
 for the acceleration to get
( 9 )
m(−4π2f2y) = −ky
from which we get an expression for the frequency f and the period T.
( 10 )
f =
1
2π
k
m
( 11 )
T = 2π
m
k
Using equation 11, we can predict the period if we know the mass on the spring and the spring constant. Alternately, knowing the mass on the spring and experimentally measuring the period, we can determine the spring constant of the spring. Notice that in equation 11, the relationship between T and m is not linear. A graph of the period versus the mass will not be a straight line. If we square both sides of equation 11, we get
( 12 )
T2 = 4π2
m
k
.
Now, a graph of
T2
 versus m will be a straight line, and the spring constant can be determined from the slope.

Simple Pendulum

The other example of simple harmonic motion that you will investigate is the simple pendulum. The simple pendulum consists of a mass m, called the pendulum bob, attached to the end of a string. The length L of the simple pendulum is measured from the point of suspension of the string to the center of the bob as shown in Figure 7 below.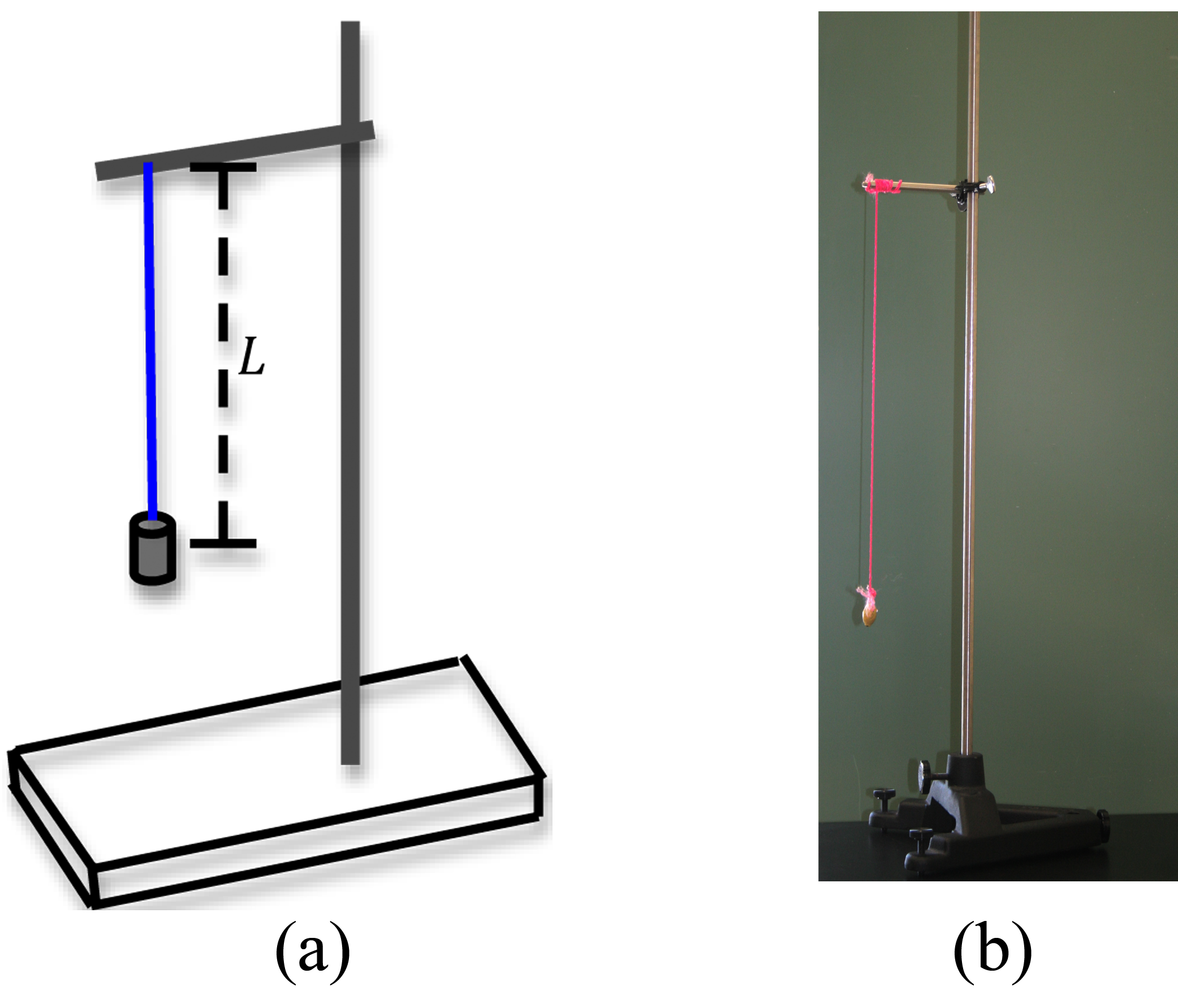
7a shows stand with hanging pendulum bob, with the length of the string labeled as L. 7b is a photograph of the same.
Figure 7: Experimental set-up for a simple pendulum
If the bob is moved away from the rest position through some angle of displacement θ as in Figure 8, the restoring force will return the bob back to the equilibrium position. The forces acting on the bob are the force of gravity and the tension force of the string. The tension force of the string is balanced by the component of the gravitational force that is in line with the string (i.e. perpendicular to the motion of the bob). The restoring force here is the tangential component of the gravitational force.
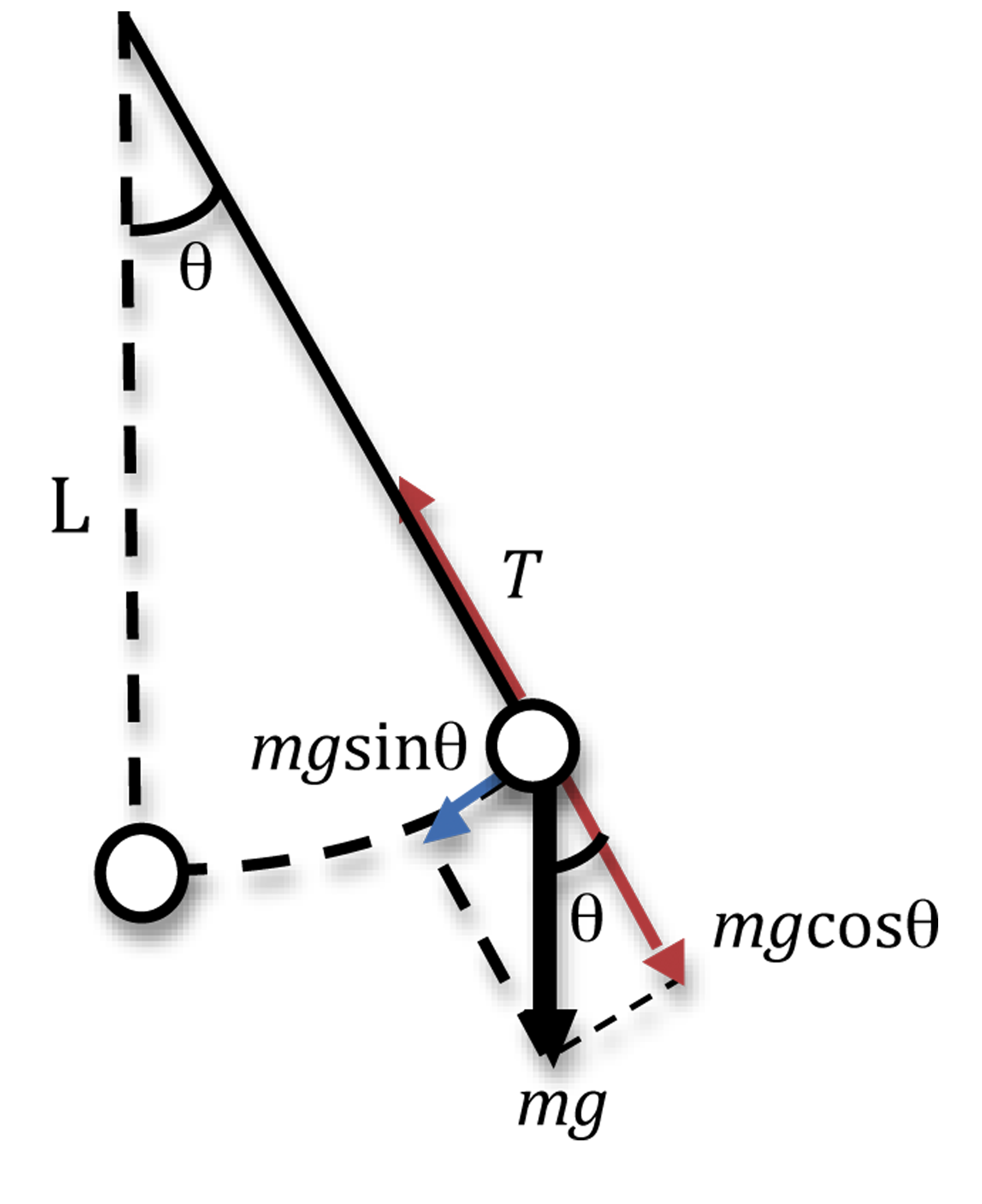
Diagram of the pendulum moving. Length of the string is denoted by L; the angle of the string's displacement is noted by theta. The vector towards the stand is given by T; vector away from the stand is given by mg cosine theta; the vector down is labeled mg; the vector towards the pendulum's original location is mg sine theta. The between mg and mg cosine theta is labeled as theta.
Figure 8: Simple pendulum
When we apply trigonometry to the smaller triangle in Figure 8, we get the magnitude of the restoring force |F| = mg sin θ. This force depends on the mass of the bob, the acceleration due to gravity g, and the sine of the angle through which the string has been pulled. Again Newton's second law must apply, so
( 13 )
ma = F = −mg sin θ
where the negative sign implies that the restoring force acts opposite to the direction of motion of the bob. Since the bob is moving along the arc of a circle, the angular acceleration is given by
α = a/L.
 From equation 13 we get
( 14 )
α = −
g
L
 sin θ.
In Figure 9, the blue solid line is a plot of sin(θ) versus θ, and the straight line is a plot of θ in degrees versus θ in radians. For small angles, these two curves are almost indistinguishable. Therefore, as long as the displacement θ is small, we can use the approximation 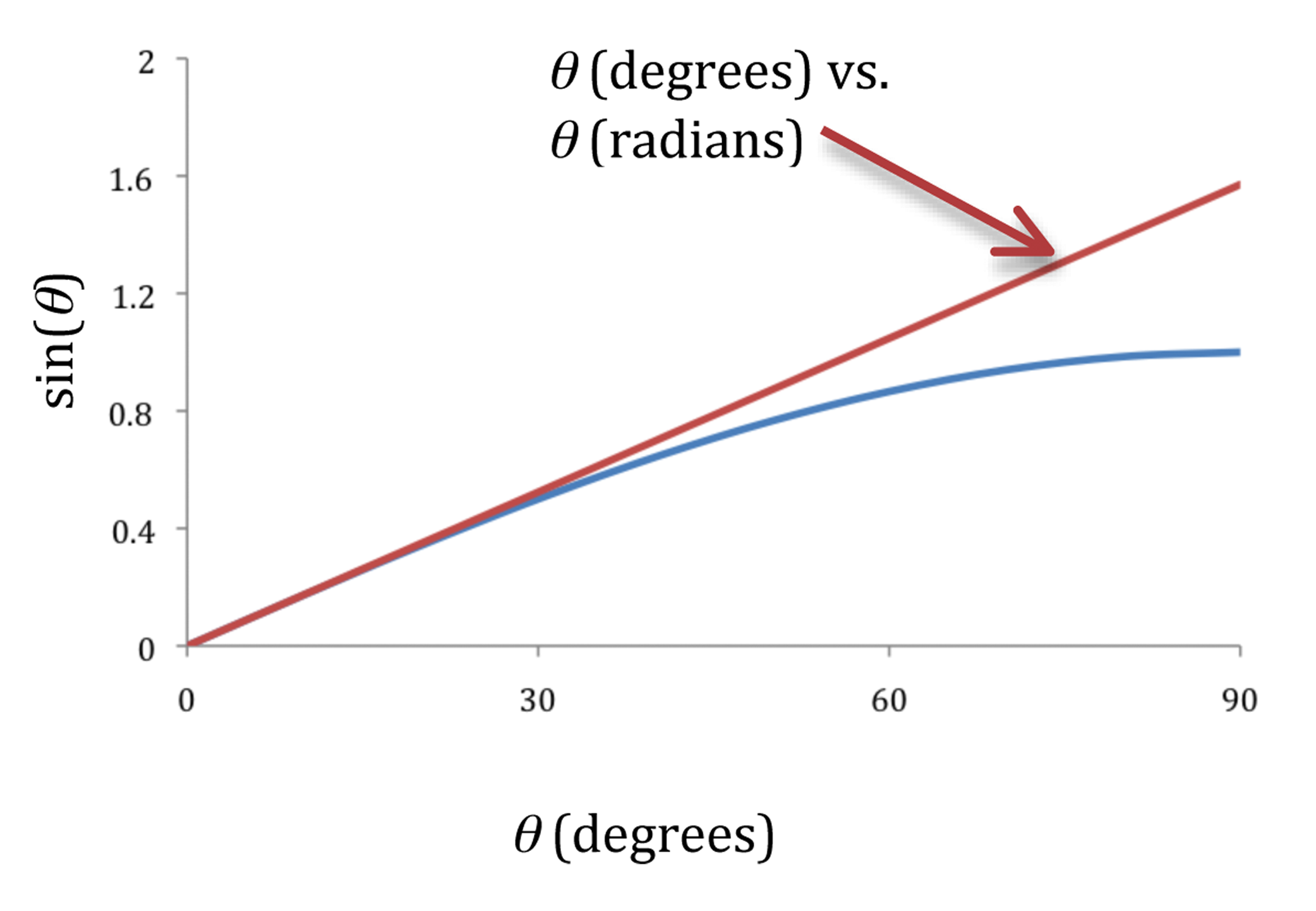sin θ ≈ θ.
Figure 9: Graphs of sin θ versus θ
With this approximation, equation 14
α = −
g
L
 sin θ.
 becomes
( 15 )
α = −
g
L
 θ.
Equation 15 shows the (angular) acceleration to be proportional to the negative of the (angular) displacement, and therefore the motion of the bob is simple harmonic and we can apply equation 5
a = −4π2f2y.
 to get
( 16 )
α = −4π2f2 θ.
Combining equation 15 and equation 16 and simplifying, we get
( 17 )
f =
1
2π
g
L
and
( 18 )
T = 2π
L
g
.
Note that the frequency and period of the simple pendulum do not depend on the mass.

Copyright © 2013 Advanced Instructional Systems, Inc. and North Carolina State University | Credits