Measurements

Units for Measurements

Chemistry is an experimental science that requires the use of a standardized system of measurements. By international agreement in 1960, scientists around the world now use SI Units (Système International d'Unités) that are based on the metric system of measurements. SI consists of seven base units (See Table 1) which, when combined or used with a series of Greek prefixes (See Table 2), leads to a series of derived units.

Figure : Table 1. Base Units of SI

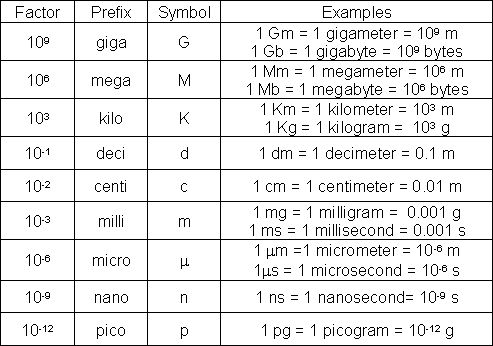
Figure : Table 2. Common SI and Metric Prefixes

The important base units commonly used in chemistry: Length: The base unit of length is the meter (m), which technically is defined as the distance light travels through a vacuum in 1/299,792,458 second, a complex standard. For most measurements in a chemical laboratory, the meter is a large unit. The derived units of centimeter (cm), millimeter (mm, about the thickness of a new US dime), micrometer or micron (

μm)

and nanometer (nm) are used. Using the values in Table 2:

1 m = 100 cm = 1000 mm = 1,000,000
μm
= 1,000,000,000 nm
OR 1 m = 10² cm = 10³ mm = 10⁶
μm
= 10⁹ nm.

Mass: The measure of the amount of matter is the mass, for which the kilogram (kg) is the base unit. Again, the base unit is too large for most measurements in a chemical laboratory, so the derived units of gram (g, about half the mass of a new US penny), milligram (mg) and microgram (

μg)

are used. Although we often use mass and weight interchangeably, they are different. Mass is the amount of matter; weight is the force exerted upon this mass by gravity. You will, for example, have the same mass on Earth as in outer space, but you will be weightless in outer space, in the absence of gravity. The confusion is exacerbated because mass units are commonly used in the metric and SI systems, but English measurements are generally expressed in pounds, a unit of weight. The English unit of mass is a slug; the SI unit of force is the Newton. Using the values in Table 2:

1 kg = 1,000 g = 1,000,000 mg = 1,000,000,000
μg
OR 1 kg = 10³ g = 10⁶ mg = 10⁹
μg
.

Temperature: The Kelvin (K, which is read as "Kelvin" and not degrees Kelvin) is the base SI unit of temperature. The Kelvin, like the more commonly used degree Celsius (°C), is one-hundredth of the interval between the freezing and boiling points of water at atmospheric pressure. They differ in the values assigned to these points; therefore

K = °C + 273.15 and °C = K
−
273.15.

A temperature of

−273.15

°C or 0.00 K is absolute zero. Mole: The mole (mol) is the SI standard measure of the amount of a substance (matter that cannot be further broken down or purified by physical means; that is, elements and compounds). A mole is the same number of "particles" (atoms, molecules, ions, etc.) as there are atoms in 12.00 g of carbon; more familiarly, this can be shown to be Avogadro's number: 6.022 × 10²³. Hence

1 mole of H = 6.022 × 10²³ atoms of H
1 mole of H₂O = 6.022 × 10²³ molecules of H₂O
1 mole of pennies = 6.022 × 10²³ pennies (more than the national debt).

Since Avogadro's number is cumbersome to work with in a laboratory, we also define the mole for an element or a compound as its mass in grams. Therefore:

1 mole of H = 6.022 × 10²³ atoms of H = 1.0079 g H (the molar mass)
1 mole of H₂O = 6.022 × 10²³ molecules of H₂O = 18.015 g H₂O (the molar mass).

Any unit that is not a base unit is a derived unit. Derived units may be formed by using the Greek prefixes with the base units, as shown in Table 2. Derived units are also formed by combining two or more of the base units. Table 3 shows some of the most common derived units.

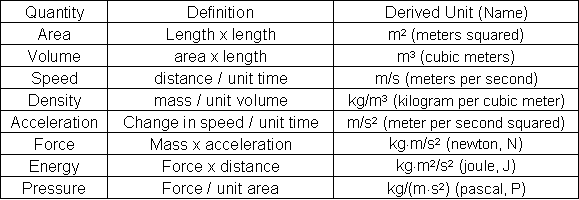
Figure : Table 3. Some Common Derived Units

Volume: Volume is the amount of space occupied by an object and is the area times the length; for a cube, this becomes length³. The common SI unit of volume is the cubic meter (m³). Because the cubic meter is a large quantity in chemical laboratory measurements, the cubic decimeter (dm³) and cubic centimeter (cm³ or cc) are used. The common name for the cubic decimeter is the liter (L) and for the cubic centimeter is the milliliter (mL). Therefore:

1 m³ = 1,000 dm³ = 1,000,000 cm³ and 1 dm³ = 1 L = 1,000 mL.

Density: Density is defined as the mass per unit volume of any substance; using base units, this is measured as kilogram per cubic meter (kg/m³). This is too large a unit for the laboratory. Thus, density is typically expressed in grams per milliliter (g/mL) or grams per cm³ (g/cm³) for liquids and solids and grams per liter (g/L) for gases. It is extremely important to ensure that units are compatible; that is, the units are not mixed SI or SI-English units. Dimensional Analysis is the process used to assure that different units of measurement are not used. For example, consider the rectangle shown in Figure 1. Before its area can be calculated, the English unit must be converted to a metric unit or vice versa.

Figure 1: A Rectangle Sized with Mixed Metric and English Units

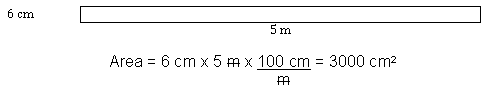
Mixed SI units must also be converted before calculations are conducted; this is usually simple in the SI system because units differ by powers of ten. Table 2 gives conversion factors. An example is given in Figure 2.

Figure 2: A Rectangle Sized with Mixed SI Units

English to metric conversion factors are available in many references. Since instruments and glassware used in chemical laboratories are seldom scaled in English units, none are given here.

Precision and Accuracy

Two terms used to express the uncertainty in measured units are precision and accuracy. Precision is a measure of how closely the data agree with each other or how close they cluster together. Accuracy is how close the measurements, or their mean, are to the actual (true) value. Data can be accurate, precise, neither, or, in the best case, both. See Figure 3 below for examples of each of these situations.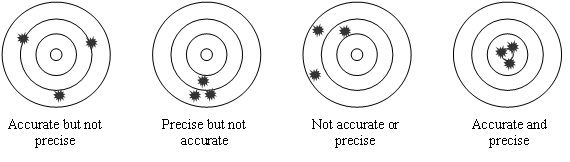

Figure 3: Diagrams Illustrating Precision and Accuracy

Significant Figures

Science recognizes two types of numbers: exact and inexact. Exact numbers are numbers that are defined such as 12 eggs in a dozen or 100 cents in a dollar or 1000 g in a kg. These numbers are known to an infinite number of significant figures and will not affect the number of significant figures when used in a calculation. Inexact numbers, however, are any number obtained by a measurement. Inexact numbers thus contain some degree of uncertainty and only have a limited number of significant figures. The degree of precision to which a measurement can be made is reflected in the way that the number is recorded. Typically all the certain digits are recorded plus one additional digit that has some degree of uncertainty in it, say

± 1.

For example,

•
A measurement of 6 indicates a reading of between 5 and 7.
•
A measurement of 6.6 indicates a reading of between 6.5 and 6.7.
•
A measurement of 6.66 indicates a reading of between 6.65 and 6.67.

There are some rules to use when determining if a digit is significant or not.

1
All non-zero digits are significant. (ex. 2.34 = 3 sig figs)
2
All zeros between non-zero digits are significant. (ex. 30.067 = 5 sig figs)
3
Zeros before the first non-zero digit are never significant; they merely indicate the position of the decimal point. (ex. 0.00089 = 2 sig figs)
4
Zeros at the end of a number and to the right of the decimal point are significant. (ex. 9.100 = 4 sig figs)
5
If a number ends in zeros but has no decimal point, the zeros may or may not be significant. In these cases, use scientific notation to clear up any ambiguity. (ex. 300 = 3 × 10² vs 300. = 3.00 × 10²)

When using inexact numbers in calculations, you must calculate the uncertainty in the resulting number. Although there are some very complicated ways to calculate uncertainty, we will simply be interested in the correct number of significant figures. There are two rules listed below. Remember, when using exact numbers such as 12 doughnuts in a dozen, 12 does not affect the number of significant figures in the result.

1
When multiplying or dividing, the result contains the same number of significant figures as the measurement with the least number of significant figures used in the calculation. (ex. 1.001 × 2.2 = 2.2022 but with only 2 significant figures due to 2.2, so the correct answer is 2.2.)
2
When adding or subtracting, the result cannot have more significant figures to the right of the decimal place than any original number. (ex. 2.023 + 4.71 = 6.733 but with only 2 decimal places due to 4.71, so the correct answer is 6.73.)

In practice, when you are carrying out a series of calculations, it is best to carry one or two extra digits through the series and round off the final result. This will help you avoid rounding errors.

Measurement Errors

Measurement errors are generally unavoidable but may be divided into two categories: random and determinate. A random error varies in a non-reproducible fashion from one measurement set to another. They usually vary in both sign and magnitude. If random errors are small they will usually affect precision but not accuracy. However, if a random error is large, it may affect the accuracy of the measurements as well, especially in a small data set. Determinate errors affect each measurement the same way and to the same extent. Therefore, they affect the accuracy more than precision. There are several types of determinate error; the two most common are systematic and proportional errors. Systematic errors are always in one direction but may be irreproducible. They usually involve difficult to control experimental conditions or instrument behavior. Calibration corrections may help these types of errors. Proportional errors involve constant relative error usually resulting from assuming some incorrect solution concentration or similar mistake. Measuring known samples (controls) at the same time can help identify this type of error.

Taking Measurements

A question often asked is "Which type of volumetric glassware should be used in performing the experiment?" The answer is given by the wording of the experimental procedure. The following instructions are useful in interpreting how to choose the volumetric glassware to be used in performing an experiment.

•
"Measure 5 mL" or "measure approximately 5 mL" indicates the use of a graduated cylinder.
•
"Measure 5.00 mL" or "measure 5 mL to the nearest 0.02 mL" indicates the use of a volumetric pipet or a buret.