Projectile Motion

Introduction

In this lab you will study the motion of a freely-falling projectile, namely a small plastic sphere. Projectile motion, for our purposes, is the motion of an object that has been launched and then is subject to only the force of gravity and the force of air friction. The Newtonian mechanics principles that you have been studying allow you to predict this type of motion quite well. You will perform two experiments to aid your understanding of these principles, which will be described later in the lab. Since there is the small but real possibility of causing injury to yourself or another person, please follow all safety guidelines and common sense safety rules.

Time-of-flight vs. Initial Velocity

The purpose of this experiment is to determine whether the time-of-flight of a ball launched horizontally off the table varies as the initial velocity is varied. A ball launched horizontally from a table of height h has no initial velocity in the vertical direction, so the ball should take the same amount of time to reach the ground as a ball that drops from rest from the same height. The kinematic equation

h = (1/2)gt²

can be used to determine the time-of-flight, which is independent of initial velocity:

( 1 )

t =

Figure 1

Projectile Motion

The purpose of this experiment is to predict and verify the range and the time-of-flight of a projectile launched at an angle.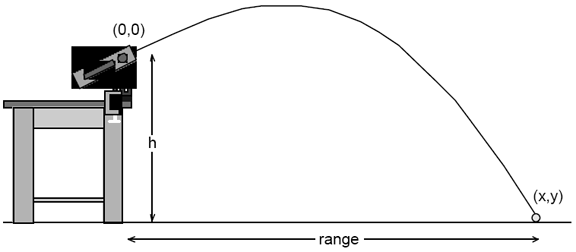

Figure 2

To predict the range of the projectile when it is shot off a table at some angle above the horizontal, it is necessary first to determine the initial speed (muzzle velocity) of the ball. The initial velocity of the ball is determined by shooting it, at the appropriate angle, through 2 photogates that are placed near the muzzle and only a few centimeters apart from each other. Then the initial velocity can be used to calculate where the ball will land when it is shot at some angle θ. Initial velocity: The photogates are approximately 10 centimeters apart (measure directly to confirm this). A Smart Timer can be used to measure the time the ball takes to travel between these two gates. The average speed between the gates can then be calculated from v = (10 cm)/time. Time-of-flight and range: To predict the total time-of-flight, you can use the vertical y-component of the initial velocity along with the initial and final y-coordinates of the ball. To predict the range, you can use the total time-of-flight and the x-component of the initial velocity. You will derive these two equations, one for the range and one for the total time-of-flight, before you actually perform the experiment. Then, you will calculate values for the range and time-of-flight using your equations. After you calculate the expected values, you will perform the experiment to see if you calculated correctly!

Procedure

General Operation of the Projectile Launcher

Caution:
Safety glasses must be worn during this experiment.

Caution:
When the projectile launcher is loaded, a yellow indicator is visible in one of the range slots in the side of the barrel and the ball is visible in another one of the slots in the side of the barrel. As with all projectile launching mechanisms, NEVER LOOK DOWN THE BARREL WHEN IT IS LOADED. To check to see if the launcher is loaded, always check the side of the barrel.

Before shooting the ball, make certain no one is in its flight path. To shoot the ball, pull straight up on the string that is attached to the trigger. It is only necessary to pull it about a centimeter.

Time-of-flight vs. Initial Velocity

Equipment Set-Up

The launchers should be set up when you arrive; do not adjust the placement of the launchers unless instructed to do so by your TA. Each launcher should be clamped to the edge of a lab bench and aimed so that the ball will land on the floor without hitting any other lab groups.

1
Adjust the angle of the projectile launcher to zero degrees (0°).
2
Connect the lead from the photogate closest to the muzzle of the launcher into port 1 on the right side of the Smart Timer.
3
Plug the time-of-flight plate into port 2 of the Smart Timer.
4
Turn on the Smart Timer and select Time and Two Gates mode. Press the Start button on the Smart Timer, and an asterisk (*) should appear indicating that the device is ready to collect data. Now, as the ball leaves the muzzle of the launcher, it signals the timer to start timing when it passes through the first gate. When it lands on the time-of-flight plate, a second signal is sent to the timer that tells it to stop. The time recorded is the time-of-flight.

Note: If the timer does not start, the photogate beam may be blocked by the launcher, in which case the bracket should be moved outward so that the first photogate is just beyond the front end of the launcher.

Time-of-Flight

1
Put on your safety glasses.
2
Measure the vertical distance from the bottom of the ball's launch position in the barrel (this position is marked on one side of the barrel) to the top of the strike plate.
3
Put the yellow plastic ball into the projectile launcher and cock it to the short range position.
4
Test fire the ball to determine where to place the time-of-flight plate. Put the time-of-flight plate on the floor where the ball lands. Make sure it hits ONLY in the white area on the plate and that the path of the ball is parallel to the longest side of the white area. Practice and patience are required to ensure that the ball accurately lands on the pad and the time of flight is properly recorded.

Whenever you launch a ball, position one member of your lab group ready to catch the ball after it lands to avoid losing the ball or interfering with other students in the room.

5
Fire five shots and record the time-of-flight for each trial. Remember to push the Start/Stop button on the photogate timer before firing.
6
Measure and record the horizontal distance (range) traveled by the ball.
7
Repeat steps 3 to 6 for the medium range launch position.

You should observe that the time of flight does not depend on the initial velocity when the ball is launched horizontally. Calculate the initial velocity for each of the two launch settings from

v_o = Δx/Δt,

where Δx is the range or horizontal displacement of the ball.

Projectile Motion

Measuring the Initial Velocity Directly

1
Set the angle of the launcher to 0°.
2
Disconnect the time-of-flight plate from the Smart Timer, and connect the second photogate in port 2 so that the timer will now record the time for the ball to pass between the two gates.
3
Load the ball into the short range setting, reset the timer, and launch the ball. Record the time taken for the ball to travel between the gates.
4
Calculate the initial velocity, v_o, using the distance and time between the gates.
5
Repeat steps 3 and 4 several times and calculate the average initial velocity and uncertainty.

Predicting and Verifying the Range and Total Time-of-Flight

Use the equations you derived in the Pre-lab Assignment to calculate the expected range and time-of-flight using your best estimate of the average initial velocity for the short range setting, and the launch angle. To test your predictions, follow the steps outlined below.

1
Adjust the angle of the launcher to 30 degrees. Use a binder clip to hold a piece of paper to the time-of-flight pad, and place a piece of carbon paper (carbon side down) on top. Place the time-of-flight pad at the spot you predict the ball to land. You will also want to record the time-of-flight: unplug the second gate from the Smart Timer and plug in the cord from the time-of-flight pad.
2
Test fire the ball. If you miss the time-of-flight pad, check your calculations and try again!
3
Launch the ball five times at 30°, and record the time-of-flight each time. To find the range for each trial, use a plumb bob to find the point on the floor that is directly beneath the release point of the ball marked on the barrel of the launcher (there is a diagram of the ball on the side of the launcher that shows the release point). Measure the horizontal distance from the point on the floor beneath the release point to each of the five landing points. If you need to move the plate between launches, remember to record the necessary range values first!

Target Challenge (optional)

For an additional challenge, your TA may place a target or basket at a specified point for you to try to hit. Use your equations to determine an appropriate launch setting to score a hit!

Analysis

Time-of-flight vs. Initial Velocity

1
Calculate the average time-of-flight and the uncertainty for the short and medium ranges.
2
Calculate the average initial velocity for the short and medium ranges.

Projectile Motion

1
Calculate the average initial velocity for the short range using the two photogates. Does this value agree with that found in Time-of-flight vs. Initial Velocity? Which method do you believe is more accurate?
2
Compare your predicted and measured ranges and flight times. Do they agree within the experimental uncertainties? If not, explain why there is a discrepancy.

Discussion

Did the time-of-flights for part one change with the initial velocity? Discuss the differences between your predicted and experimental results for both the range and time-of-flight. Is there agreement to within the uncertainties? If not, explain. Which is more significant for this lab: random or systematic errors? How can you tell? What do you believe is the primary source of uncertainty in this experiment? What would you do differently to improve your results? How significant is air resistance for this experiment? Use your experimental results to estimate the maximum relative error introduced by this factor.