Measurements and Error Analysis
"It is better to be roughly right than precisely wrong." — Alan Greenspan
The Uncertainty of Measurements
Some numerical statements are exact: Mary has 3 brothers, and 2 + 2 = 4. However, all measurements have some degree of uncertainty that may come from a variety of sources. The process of evaluating the uncertainty associated with a measurement result is often called uncertainty analysis or error analysis.
The complete statement of a measured value should include an estimate of the level of
confidence associated with the value. Properly reporting an experimental result along
with its uncertainty allows other people to make judgments about the quality of the
experiment, and it facilitates meaningful comparisons with other similar values or a
theoretical prediction. Without an uncertainty estimate, it is impossible to answer the
basic scientific question: "Does my result agree with a theoretical prediction or results
from other experiments?" This question is fundamental for deciding if a scientific
hypothesis is confirmed or refuted.
When we make a measurement, we generally assume that some exact or true value exists based on how we define what is being measured. While we may never know this true value exactly, we attempt to find this ideal quantity to the best of our ability with the
time and resources available. As we make measurements by different methods, or even when making multiple measurements using the same method, we may obtain slightly different results. So how do we report our findings for our best estimate of this elusive true value? The most common way to show the range of values that we believe includes
the true value is:
( 1 )
measurement = (best estimate ± uncertainty) units
Let's take an example. Suppose you want to find the mass of a gold ring that you
would like to sell to a friend. You do not want to jeopardize your friendship, so you want
to get an accurate mass of the ring in order to charge a fair market price. You estimate the
mass to be between 10 and 20 grams from how heavy it feels in your hand, but this is not
a very precise estimate. After some searching, you find an electronic balance that gives a
mass reading of 17.43 grams. While this measurement is much more precise than the
original estimate, how do you know that it is accurate, and how confident are you that
this measurement represents the true value of the ring's mass? Since the digital display of
the balance is limited to 2 decimal places, you could report the mass as m = 17.43 ± 0.01 g.
Suppose you use the same electronic balance and obtain several more readings: 17.46
g, 17.42 g, 17.44 g, so that the average mass appears to be in the range of 17.44 ± 0.02 g.
By now you may feel confident that you know the mass of this ring to the nearest
hundredth of a gram, but how do you know that the true value definitely lies between
17.43 g and 17.45 g? Since you want to be honest, you decide to use another balance that
gives a reading of 17.22 g. This value is clearly below the range of values found on the
first balance, and under normal circumstances, you might not care, but you want to be fair
to your friend. So what do you do now? The answer lies in knowing something about the
accuracy of each instrument.
To help answer these questions, we should first define the terms accuracy and precision:
Accuracy is the closeness of agreement between a measured value and a true or accepted value. Measurement error is the amount of inaccuracy.
Precision is a measure of how well a result can be determined (without reference to a theoretical or true value). It is the degree of consistency and agreement among independent measurements of the same quantity; also the reliability or reproducibility of the result.
The uncertainty estimate associated with a measurement should account for both the accuracy and precision of the measurement.
Note: Unfortunately the terms error and uncertainty are often used interchangeably to
describe both imprecision and inaccuracy. This usage is so common that it is impossible
to avoid entirely. Whenever you encounter these terms, make sure you understand
whether they refer to accuracy or precision, or both.
Notice that in order to determine the accuracy of a particular measurement, we have
to know the ideal, true value. Sometimes we have a "textbook" measured value, which is
well known, and we assume that this is our "ideal" value, and use it to estimate the
accuracy of our result. Other times we know a theoretical value, which is calculated from
basic principles, and this also may be taken as an "ideal" value. But physics is an
empirical science, which means that the theory must be validated by experiment, and not
the other way around. We can escape these difficulties and retain a useful definition of
accuracy by assuming that, even when we do not know the true value, we can rely on the
best available accepted value with which to compare our experimental value.
For our example with the gold ring, there is no accepted value with which to compare,
and both measured values have the same precision, so we have no reason to believe one
more than the other. We could look up the accuracy specifications for each balance as
provided by the manufacturer (the Appendix at the end of this lab manual contains accuracy data for most instruments you will use), but the best way to assess the accuracy
of a measurement is to compare with a known standard. For this situation, it may be
possible to calibrate the balances with a standard mass that is accurate within a narrow
tolerance and is traceable to a primary mass standard at the National Institute of
Standards and Technology (NIST). Calibrating the balances should eliminate the
discrepancy between the readings and provide a more accurate mass measurement.
Precision is often reported quantitatively by using relative or fractional uncertainty:
( 2 )
Relative Uncertainty =
| uncertainty |
| measured quantity |
Example: m = 75.5 ± 0.5 g
has a fractional uncertainty of:
Accuracy is often reported quantitatively by using relative error:
( 3 )
Relative Error =
| measured value − expected value |
| expected value |
If the expected value for m is 80.0 g, then the relative error is:
Note: The minus sign indicates that the measured value is less than the expected
value.
When analyzing experimental data, it is important that you understand the difference between precision and accuracy. Precision indicates the quality of the measurement, without any guarantee that the measurement is "correct." Accuracy, on the other hand, assumes that there is an ideal value, and tells how far your answer is from that ideal, "right" answer. These concepts are directly related to random and systematic measurement errors.
Types of Errors
Measurement errors may be classified as either random or systematic, depending on how the measurement was obtained (an instrument could cause a random error in one situation and a systematic error in another).
Random errors are statistical fluctuations (in either direction) in the measured data due to the precision limitations of the measurement device. Random errors can be evaluated through statistical analysis and can be reduced by averaging over a large number of observations (see standard error).
Systematic errors are reproducible inaccuracies that are consistently in the same direction. These errors are difficult to detect and cannot be analyzed statistically. If a systematic error is identified when calibrating against a standard, applying a correction or correction factor to
compensate for the effect can reduce the bias. Unlike random errors, systematic errors cannot be detected or reduced by increasing the number of observations.
When making careful measurements, our goal is to reduce as many sources of error as possible and to keep track of those errors that we can not eliminate. It is useful to know the types of errors that may occur, so that we may recognize them when they arise. Common sources of error in physics laboratory experiments:
Incomplete definition (may be systematic or random) — One reason that it is impossible
to make exact measurements is that the measurement is not always clearly defined. For
example, if two different people measure the length of the same string, they would
probably get different results because each person may stretch the string with a different
tension. The best way to minimize definition errors is to carefully consider and specify
the conditions that could affect the measurement.
Failure to account for a factor (usually systematic) — The most challenging part of
designing an experiment is trying to control or account for all possible factors except the
one independent variable that is being analyzed. For instance, you may inadvertently
ignore air resistance when measuring free-fall acceleration, or you may fail to account for
the effect of the Earth's magnetic field when measuring the field near a small magnet.
The best way to account for these sources of error is to brainstorm with your peers about
all the factors that could possibly affect your result. This brainstorm should be done
before beginning the experiment in order to plan and account for the confounding factors
before taking data. Sometimes a correction can be applied to a result after taking data to
account for an error that was not detected earlier.
Environmental factors (systematic or random) — Be aware of errors introduced by your
immediate working environment. You may need to take account for or protect your
experiment from vibrations, drafts, changes in temperature, and electronic noise or other
effects from nearby apparatus.
Instrument resolution (random) — All instruments have finite precision that limits the
ability to resolve small measurement differences. For instance, a meter stick cannot be
used to distinguish distances to a precision much better than about half of its smallest
scale division (0.5 mm in this case). One of the best ways to obtain more precise
measurements is to use a null difference method instead of measuring a quantity directly.
Null or balance methods involve using instrumentation to measure the difference between
two similar quantities, one of which is known very accurately and is adjustable. The
adjustable reference quantity is varied until the difference is reduced to zero. The two
quantities are then balanced and the magnitude of the unknown quantity can be found by
comparison with a measurement standard. With this method, problems of source
instability are eliminated, and the measuring instrument can be very sensitive and does
not even need a scale.
Calibration (systematic) — Whenever possible, the calibration of an instrument should be
checked before taking data. If a calibration standard is not available, the accuracy of the
instrument should be checked by comparing with another instrument that is at least as
precise, or by consulting the technical data provided by the manufacturer. Calibration
errors are usually linear (measured as a fraction of the full scale reading), so that larger
values result in greater absolute errors.
Zero offset (systematic) — When making a measurement with a micrometer caliper,
electronic balance, or electrical meter, always check the zero reading first. Re-zero the
instrument if possible, or at least measure and record the zero offset so that readings can
be corrected later. It is also a good idea to check the zero reading throughout the
experiment. Failure to zero a device will result in a constant error that is more significant
for smaller measured values than for larger ones.
Physical variations (random) — It is always wise to obtain multiple measurements over
the widest range possible. Doing so often reveals variations that might otherwise go
undetected. These variations may call for closer examination, or they may be combined
to find an average value.
Parallax (systematic or random) — This error can occur whenever there is some distance
between the measuring scale and the indicator used to obtain a measurement. If the
observer's eye is not squarely aligned with the pointer and scale, the reading may be too
high or low (some analog meters have mirrors to help with this alignment).
Instrument drift (systematic) — Most electronic instruments have readings that drift over
time. The amount of drift is generally not a concern, but occasionally this source of error
can be significant.
Lag time and hysteresis (systematic) — Some measuring devices require time to reach
equilibrium, and taking a measurement before the instrument is stable will result in a measurement that is too high or low. A common example is taking temperature readings with a thermometer that has not reached thermal equilibrium with its environment. A similar effect is hysteresis where the instrument readings lag behind and appear to have a "memory" effect, as data are taken sequentially moving up or down through a range of values. Hysteresis is most commonly associated with materials that become magnetized when a changing magnetic field is applied.
Personal errors come from carelessness, poor technique, or bias on the part of the experimenter. The experimenter may measure incorrectly, or may use poor technique in taking a measurement, or may introduce a bias into measurements by expecting (and inadvertently forcing) the results to agree with the expected outcome.
Gross personal errors, sometimes called mistakes or blunders, should be avoided and corrected if discovered. As a rule, personal errors are excluded from the error analysis discussion because it is generally assumed that the experimental result was obtained by following correct procedures. The term human error should also be avoided in error analysis discussions because it is too general to be useful.
Estimating Experimental Uncertainty for a Single Measurement
Any measurement you make will have some uncertainty associated with it, no matter the precision of your measuring tool. So how do you determine and report this uncertainty?
The uncertainty of a single measurement is limited by the precision and accuracy of the measuring instrument, along with any other factors that might affect the ability of the experimenter to make the measurement.
For example, if you are trying to use a meter stick to measure the diameter of a tennis ball, the uncertainty might be ± 5 mm,
but if you used a Vernier caliper, the uncertainty could be reduced to maybe ± 2 mm.
The limiting factor with the meter stick is parallax,
while the second case is limited by ambiguity in the definition of the tennis ball's diameter (it's fuzzy!). In both of these cases, the uncertainty is greater than the smallest divisions marked on the measuring tool (likely 1 mm and 0.05 mm respectively). Unfortunately, there is no general rule for determining the uncertainty in all measurements. The experimenter is the one who can best evaluate and quantify the uncertainty of a measurement based on all the possible factors that affect the result. Therefore, the person making the measurement has the obligation to make the best judgment possible and report the uncertainty in a way that clearly explains what the uncertainty represents:
( 4 )
Measurement = (measured value ±
standard uncertainty) unit of measurement
where the ± standard uncertainty indicates approximately a 68% confidence interval (see sections on Standard Deviation and Reporting Uncertainties).
Example: Diameter of tennis ball = 6.7 ± 0.2 cm.
Estimating Uncertainty in Repeated Measurements
Suppose you time the period of oscillation of a pendulum using a digital instrument (that you assume is measuring accurately) and find: T = 0.44 seconds. This single measurement of the period suggests a precision of ±0.005 s, but this instrument precision may not give a complete sense of the uncertainty. If you repeat the measurement several times and examine the variation among the measured values, you can get a better idea of the uncertainty in the period. For example, here are the results of 5 measurements, in seconds: 0.46, 0.44, 0.45, 0.44, 0.41.
( 5 )
Average (mean) =
x1 + x2 +  + xN + xN |
| N |
For this situation, the best estimate of the period is the average, or mean.
Whenever possible, repeat a measurement several times and average the
results. This average is generally the best estimate of the "true" value
(unless the data set is skewed by one or more outliers which should be
examined to determine if they are bad data points that should be omitted
from the average or valid measurements that require further investigation).
Generally, the more repetitions you make of a measurement, the better this
estimate will be, but be careful to avoid wasting time taking more
measurements than is necessary for the precision required.
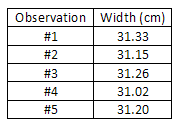
Consider, as another example, the measurement of the width of a piece of paper using
a meter stick. Being careful to keep the meter stick parallel to the edge of the paper (to
avoid a systematic error which would cause the measured value to be consistently higher
than the correct value), the width of the paper is measured at a number of points on the
sheet, and the values obtained are entered in a data table. Note that the last digit is only a
rough estimate, since it is difficult to read a meter stick to the nearest tenth of a millimeter
(0.01 cm).
( 6 )
Average =
| sum of observed widths |
| no. of observations |
=
= 31.19 cm
This average is the best available estimate of the width of the piece of paper, but it is
certainly not exact. We would have to average an infinite number of measurements to
approach the true mean value, and even then, we are not guaranteed that the mean value is
accurate because there is still some systematic error from the measuring tool, which can
never be calibrated perfectly. So how do we express the uncertainty in our average value?
One way to express the variation among the measurements is to use the average
deviation. This statistic tells us on average (with 50% confidence) how much the
individual measurements vary from the mean.
( 7 )
d =
|x1 − x| + |x2 − x| +  + |xN − x| + |xN − x| |
| N |
However, the standard deviation is the most common way to characterize the spread
of a data set. The standard deviation is always slightly greater than the average deviation, and is used because of its association with the normal distribution that is frequently encountered in statistical analyses.
Standard Deviation
To calculate the standard deviation for a sample of N measurements:
-
1
Sum all the measurements and divide by N to get the average, or mean.
-
2
Now, subtract this average from each of the N measurements to obtain N "deviations".
-
3
Square each of these N deviations and add them all up.
-
4
Divide this result by (N − 1)
and take the square root.
We can write out the formula for the standard deviation as follows. Let the N measurements be called x1, x2, ..., xN. Let the average of the N values be called x.
Then
each deviation is given by δxi =
xi −
x, for
i = 1, 2,

,
N.
The standard deviation is:
In our previous example, the average width x
is 31.19 cm. The deviations are:
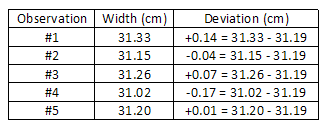 The average deviation is:
The average deviation is: d = 0.086 cm.
The standard deviation is: s =
 | | (0.14)2 + (0.04)2 + (0.07)2 + (0.17)2 + (0.01)2 | | 5 − 1 |
|
= 0.12 cm.
The significance of the standard deviation is this: if you now make one more measurement using the same meter stick, you can reasonably expect (with about 68% confidence) that the new measurement will be within 0.12 cm of the estimated average of 31.19 cm. In fact, it is reasonable to use the standard deviation as the uncertainty associated with this single new measurement. However, the uncertainty of the average value is the standard deviation of the mean, which is always less than the standard deviation (see next section).
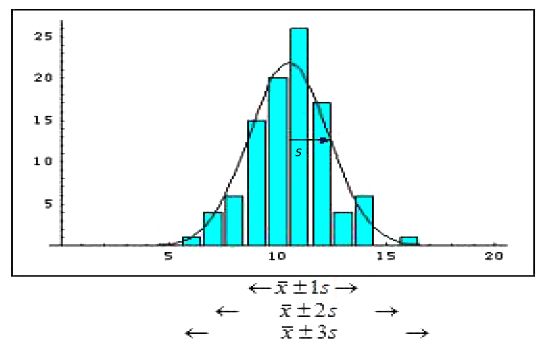
Consider an example where 100 measurements of a quantity were made. The average or mean value was 10.5 and the standard deviation was s = 1.83. The figure below is a histogram of the 100 measurements, which shows how often a certain range of values
was measured. For example, in 20 of the measurements, the value was in the range 9.5 to 10.5, and most of the readings were close to the mean value of 10.5. The standard deviation s for this set of measurements is roughly how far from the average value most of the readings fell. For a large enough sample, approximately 68% of the readings will
be within one standard deviation of the mean value, 95% of the readings will be in the interval x ± 2 s,
and nearly all (99.7%) of readings will lie within 3 standard deviations from the mean. The smooth curve superimposed on the histogram is the gaussian or
normal distribution predicted by theory for measurements involving random errors. As more and more measurements are made, the histogram will more closely follow the bellshaped gaussian curve, but the standard deviation of the distribution will remain approximately the same.
Standard Deviation of the Mean (Standard Error)
When we report the average value of N measurements, the uncertainty we should
associate with this average value is the standard deviation of the mean, often called the
standard error (SE).
( 9 )
σx =
| s |
 | N |
|
The standard error is smaller than the standard deviation by a factor of 1/
 | N |
.
 | 5 |
.
Average paper width = 31.19 ± 0.05 cm.
Anomalous Data
The first step you should take in analyzing data (and even while taking data) is to examine the data set as a whole to look for patterns and outliers. Anomalous data points
that lie outside the general trend of the data may suggest an interesting phenomenon that
could lead to a new discovery, or they may simply be the result of a mistake or random
fluctuations. In any case, an outlier requires closer examination to determine the cause of
the unexpected result. Extreme data should never be "thrown out" without clear
justification and explanation, because you may be discarding the most significant part of
the investigation! However, if you can clearly justify omitting an inconsistent data point,
then you should exclude the outlier from your analysis so that the average value is not
skewed from the "true" mean.
Fractional Uncertainty Revisited
When a reported value is determined by taking the average of a set of independent readings, the fractional uncertainty is given by the ratio of the uncertainty divided by the average value. For this example,
( 10 )
Fractional uncertainty =
=
= 0.0016 ≈ 0.2%
Note that the fractional uncertainty is dimensionless but is often reported as a percentage or in parts per million (ppm) to emphasize the fractional nature of the value. A scientist might also make the statement that this measurement "is good to about 1 part in 500" or "precise to about 0.2%".
The fractional uncertainty is also important because it is used in propagating uncertainty in calculations using the result of a measurement, as discussed in the next section.
Propagation of Uncertainty
Suppose we want to determine a quantity f, which depends on x and maybe several other variables y, z, etc. We want to know the error in f if we measure x, y, ... with errors σx, σy, ...
Examples:
( 11 )
f = xy (Area of a rectangle)
( 12 )
f = p cos θ (x-component of momentum)
( 13 )
f = x/t (velocity)
For a single-variable function f(x), the deviation in f can be related to the deviation in
x using calculus:
Thus, taking the square and the average:
( 15 )
δf2 =
 | 2 |
| |
δx2
and using the definition of σ, we get:
Examples:
(a) f =
 | x |
( 17 )
=
| 1 |
2 | x |
|
( 18 )
σf =
| σx |
2 | x |
|
, or
=
(b) f = x2
(c) f = cos θ
( 22 )
σf = |sin
θ|
σθ, or
= |tan
θ|
σθ
Note: in this situation, σθ must be in radians.
In the case where f depends on two or more variables, the derivation above can be
repeated with minor modification. For two variables, f(x, y), we have:
The partial derivative
means differentiating f with respect to x holding the other
variables fixed. Taking the square and the average, we get the law of propagation of
uncertainty:
( 24 )
(
δf)
2 =
 | 2 |
| |
(
δx)
2 +
 | 2 |
| |
(
δy)
2 + 2
δx δy
If the measurements of x and y are uncorrelated, then δx δy = 0,
and we get:
( 25 )
σf =
 | 2 σx2 + 2 σy2 |
Examples:
(a) f = x + y
( 27 )
∴
σf =
 | σx2 + σy2 |
When adding (or subtracting) independent measurements, the absolute uncertainty of the
sum (or difference) is the root sum of squares (RSS) of the individual absolute uncertainties. When adding correlated measurements, the uncertainty in the result is simply the sum of the
absolute uncertainties, which is always a larger uncertainty estimate than adding in
quadrature (RSS). Adding or subtracting a constant does not change the absolute uncertainty
of the calculated value as long as the constant is an exact value.
(b) f = xy
( 29 )
∴
σf =
 | y2σx2 + x2σy2 |
Dividing the previous equation by f = xy, we get:
( 30 )
=
 | 2 + 2 |
(c) f = x/y
( 32 )
∴
σf =
 | 2σx2 + 2σy2 |
Dividing the previous equation by f = x/y,
we get:
( 33 )
=
 | 2 + 2 |
When multiplying (or dividing) independent measurements, the relative uncertainty of the
product (quotient) is the RSS of the individual relative uncertainties. When multiplying
correlated measurements, the uncertainty in the result is just the sum of the relative uncertainties,
which is always a larger uncertainty estimate than adding in quadrature (RSS). Multiplying or
dividing by a constant does not change the relative uncertainty of the calculated value.
Note that the relative uncertainty in f, as shown in (b) and (c) above, has the same
form for multiplication and division: the relative uncertainty in a product or quotient
depends on the relative uncertainty of each individual term.
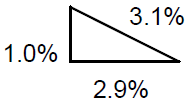
Example: Find uncertainty in v, where v = at
with a = 9.8 ± 0.1 m/s2, t = 1.2 ± 0.1 s
( 34 )
=
 | 2 + 2 |
=
 | + |
=
 | (0.010)2 + (0.029)2 |
= 0.031 or 3.1%
Notice that the relative uncertainty in t (2.9%) is significantly greater than the relative
uncertainty for a (1.0%), and therefore the relative uncertainty in v is essentially the same
as for t (about 3%).
Graphically, the RSS is like the Pythagorean theorem:
The total uncertainty is the length of the hypotenuse of a right triangle with legs the length of each uncertainty component.
Timesaving approximation: "A chain is only as strong as its weakest
link."
If one of the uncertainty terms is more than 3 times greater than the other
terms, the root-squares formula can be skipped, and the combined
uncertainty is simply the largest uncertainty. This shortcut can save a lot of
time without losing any accuracy in the estimate of the overall uncertainty.
The Upper-Lower Bound Method of Uncertainty Propagation
An alternative, and sometimes simpler procedure, to the tedious propagation of
uncertainty law is the upper-lower bound method of uncertainty propagation. This
alternative method does not yield a standard uncertainty estimate (with a 68% confidence
interval), but it does give a reasonable estimate of the uncertainty for practically any
situation. The basic idea of this method is to use the uncertainty ranges of each variable to
calculate the maximum and minimum values of the function. You can also think of this
procedure as examining the best and worst case scenarios. For example, suppose you
measure an angle to be: θ = 25° ± 1° and you needed to find f = cos θ, then:
( 35 )
fmax = cos(26°) = 0.8988
( 36 )
fmin = cos(24°) = 0.9135
( 37 )
∴
f = 0.906 ±
0.007 where 0.007 is half the difference between
fmax and
fmin
Note that even though θ was only measured to 2 significant figures, f is known to 3
figures. By using the propagation of uncertainty law: σf = |sin θ|σθ = (0.423)(π/180) = 0.0074
(same result as above).
The uncertainty estimate from the upper-lower bound method is generally
larger than the standard uncertainty estimate found from the propagation of
uncertainty law, but both methods will give a reasonable estimate of the
uncertainty in a calculated value.
The upper-lower bound method is especially useful when the functional relationship
is not clear or is incomplete. One practical application is forecasting the expected range in
an expense budget. In this case, some expenses may be fixed, while others may be
uncertain, and the range of these uncertain terms could be used to predict the upper and
lower bounds on the total expense.
Significant Figures
The number of significant figures in a value can be defined as all the digits between
and including the first non-zero digit from the left, through the last digit. For instance,
0.44 has two significant figures, and the number 66.770 has 5 significant figures. Zeroes
are significant except when used to locate the decimal point, as in the number 0.00030,
which has 2 significant figures. Zeroes may or may not be significant for numbers like
1200, where it is not clear whether two, three, or four significant figures are indicated. To avoid this ambiguity, such numbers should be expressed in scientific notation to (e.g.
1.20 × 103 clearly indicates three significant figures).
When using a calculator, the display will often show many digits, only some of which
are meaningful (significant in a different sense). For example, if you want to estimate the
area of a circular playing field, you might pace off the radius to be 9 meters and use the
formula: A = πr2. When you compute this area, the calculator might report a value of
254.4690049 m2. It would be extremely misleading to report this number as the area of
the field, because it would suggest that you know the area to an absurd degree of
precision—to within a fraction of a square millimeter! Since the radius is only known to
one significant figure, the final answer should also contain only one significant figure:
Area = 3 × 102 m2.
From this example, we can see that the number of significant figures reported for a
value implies a certain degree of precision. In fact, the number of significant figures
suggests a rough estimate of the relative uncertainty:
The number of significant figures implies an approximate relative
uncertainty:
1 significant figure suggests a relative uncertainty of about 10% to 100%
2 significant figures suggest a relative uncertainty of about 1% to 10%
3 significant figures suggest a relative uncertainty of about 0.1% to 1%
To understand this connection more clearly, consider a value with 2 significant
figures, like 99, which suggests an uncertainty of ±1, or a relative uncertainty of ±1/99 = ±1%. (Actually some people might argue that the implied uncertainty in 99 is ±0.5 since the range of values that would round to 99 are 98.5 to 99.4. But since the uncertainty here
is only a rough estimate, there is not much point arguing about the factor of two.) The
smallest 2-significant figure number, 10, also suggests an uncertainty of ±1, which in this case is a relative uncertainty of ±1/10 = ±10%. The ranges for other numbers of significant figures can be reasoned in a similar manner.
Use of Significant Figures for Simple Propagation of Uncertainty
By following a few simple rules, significant figures can be used to find the
appropriate precision for a calculated result for the four most basic math functions, all
without the use of complicated formulas for propagating uncertainties.
For multiplication and division, the number of significant figures that are
reliably known in a product or quotient is the same as the smallest number
of significant figures in any of the original numbers.
Example:
| 6.6 | | |
| × | 7328.7 | | |
| 48369.42 | = | 48 × 103 |
| (2 significant figures) |
| (5 significant figures) |
| (2 significant figures) |
For addition and subtraction, the result should be rounded off to the last decimal place reported for the least precise number.
Examples:
| 223.64 | | | 5560.5 |
| + | 54 | | + | 0.008 |
| | 278 | | | 5560.5 |
If a calculated number is to be used in further calculations, it is good practice to keep
one extra digit to reduce rounding errors that may accumulate. Then the final answer
should be rounded according to the above guidelines.
Uncertainty, Significant Figures, and Rounding
For the same reason that it is dishonest to report a result with more significant figures
than are reliably known, the uncertainty value should also not be reported with excessive
precision.
For example, it would be unreasonable for a student to report a result like:
( 38 )
measured density = 8.93 ± 0.475328 g/cm3 WRONG!
The uncertainty in the measurement cannot possibly be known so precisely! In most
experimental work, the confidence in the uncertainty estimate is not much better than
about ±50% because of all the various sources of error, none of which can be known
exactly. Therefore, uncertainty values should be stated to only one significant figure (or
perhaps 2 sig. figs. if the first digit is a 1).
Because experimental uncertainties are inherently imprecise, they should
be rounded to one, or at most two, significant figures.
To help give a sense of the amount of confidence that can be placed in the standard
deviation, the following table indicates the relative uncertainty associated with the
standard deviation for various sample sizes. Note that in order for an uncertainty value to
be reported to 3 significant figures, more than 10,000 readings would be required to
justify this degree of precision!
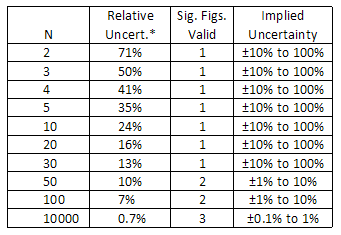 *The relative uncertainty is given by the approximate formula:
*The relative uncertainty is given by the approximate formula: =
| 1 |
 | 2(N − 1) |
|
When an explicit uncertainty estimate is made, the uncertainty term indicates how many significant figures should be reported in the measured value
(not the other way around!). For example, the uncertainty in the density measurement
above is about 0.5 g/cm3, so this tells us that the digit in the tenths place is uncertain, and
should be the last one reported. The other digits in the hundredths place and beyond are
insignificant, and should not be reported: measured density = 8.9 ± 0.5 g/cm3.
RIGHT!
An experimental value should be rounded to be consistent with the
magnitude of its uncertainty. This generally means that the last significant
figure in any reported value should be in the same decimal place as the
uncertainty.
In most instances, this practice of rounding an experimental result to be consistent
with the uncertainty estimate gives the same number of significant figures as the rules
discussed earlier for simple propagation of uncertainties for adding, subtracting,
multiplying, and dividing.
Caution: When conducting an experiment, it is important to keep in mind that
precision is expensive (both in terms of time and material resources). Do not waste your
time trying to obtain a precise result when only a rough estimate is required. The cost
increases exponentially with the amount of precision required, so the potential benefit of
this precision must be weighed against the extra cost.
Combining and Reporting Uncertainties
In 1993, the International Standards Organization (ISO) published the first official
worldwide Guide to the Expression of Uncertainty in Measurement. Before this time,
uncertainty estimates were evaluated and reported according to different conventions
depending on the context of the measurement or the scientific discipline. Here are a few
key points from this 100-page guide, which can be found in modified form on the NIST website.
When reporting a measurement, the measured value should be reported along with an
estimate of the total combined standard uncertainty Uc
of the value. The total
uncertainty is found by combining the uncertainty components based on the two types of
uncertainty analysis:
-
Type A evaluation of standard uncertainty - method of evaluation of uncertainty
by the statistical analysis of a series of observations. This method primarily includes
random errors.
-
Type B evaluation of standard uncertainty - method of evaluation of uncertainty
by means other than the statistical analysis of series of observations. This method
includes systematic errors and any other uncertainty factors that the experimenter believes
are important.
The individual uncertainty components ui should be combined using the law of
propagation of uncertainties, commonly called the "root-sum-of-squares" or "RSS"
method. When this is done, the combined standard uncertainty should be equivalent to the
standard deviation of the result, making this uncertainty value correspond with a 68% confidence interval. If a wider confidence interval is desired, the uncertainty can be
multiplied by a coverage factor (usually k = 2 or 3) to provide an uncertainty range that
is believed to include the true value with a confidence of 95% (for k = 2) or 99.7% (for k = 3). If a coverage factor is used, there should be a clear explanation of its meaning so
there is no confusion for readers interpreting the significance of the uncertainty value.
You should be aware that the ± uncertainty notation may be used to indicate different
confidence intervals, depending on the scientific discipline or context. For example, a
public opinion poll may report that the results have a margin of error of ±3%, which means that readers can be 95% confident (not 68% confident) that the reported results are
accurate within 3 percentage points. Similarly, a manufacturer's tolerance rating
generally assumes a 95% or 99% level of confidence.
Conclusion: "When do measurements agree with each other?"
We now have the resources to answer the fundamental scientific question that was asked at the beginning of this error analysis discussion: "Does my result agree with a theoretical prediction or results from other experiments?"
Generally speaking, a measured result agrees with a theoretical prediction if the prediction lies within the range of experimental uncertainty. Similarly, if two measured values have standard uncertainty ranges that overlap, then the measurements are said to be consistent (they agree). If the uncertainty ranges do not overlap, then the
measurements are said to be discrepant (they do not agree). However, you should recognize that these overlap criteria can give two opposite answers depending on the evaluation and confidence level of the uncertainty. It would be unethical to arbitrarily
inflate the uncertainty range just to make a measurement agree with an expected value. A
better procedure would be to discuss the size of the difference between the measured and
expected values within the context of the uncertainty, and try to discover the source of the
discrepancy if the difference is truly significant. To examine your own data, you are
encouraged to use the Measurement Comparison tool available on the lab website.
Here are some examples using this graphical analysis tool:
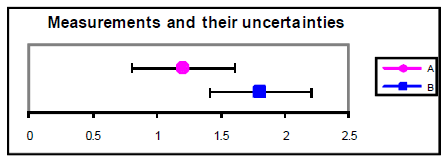
A = 1.2 ± 0.4
B = 1.8 ± 0.4
These measurements agree within
their uncertainties, despite the fact that
the percent difference between their
central values is 40%.
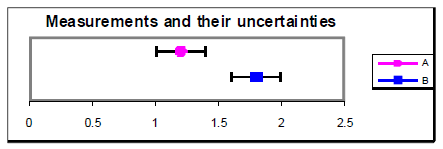
However, with half the uncertainty ± 0.2, these same measurements do not agree since their
uncertainties do not overlap. Further investigation
would be needed to determine the cause for the
discrepancy. Perhaps the uncertainties were
underestimated, there may have been a systematic
error that was not considered, or there may be a true difference between these values.
An alternative method for determining agreement between values is to calculate the
difference between the values divided by their combined standard uncertainty. This ratio
gives the number of standard deviations separating the two values. If this ratio is less
than 1.0, then it is reasonable to conclude that the values agree. If the ratio is more than
2.0, then it is highly unlikely (less than about 5% probability) that the values are the
same.
Example from above with Therefore, A and B likely agree.
Example from above with Therefore, it is unlikely that A
and B agree.
References
Baird, D.C. Experimentation: An Introduction to Measurement Theory and Experiment
Design, 3rd. ed. Prentice Hall: Englewood Cliffs, 1995.
Bevington, Phillip and Robinson, D. Data Reduction and Error Analysis for the Physical
Sciences, 2nd. ed. McGraw-Hill: New York, 1991.
ISO. Guide to the Expression of Uncertainty in Measurement. International Organization
for Standardization (ISO) and the International Committee on Weights and Measures
(CIPM): Switzerland, 1993.
Lichten, William. Data and Error Analysis., 2nd. ed. Prentice Hall: Upper Saddle River,
NJ, 1999.
NIST. Essentials of Expressing Measurement Uncertainty.
http://physics.nist.gov/cuu/Uncertainty/
Taylor, John. An Introduction to Error Analysis, 2nd. ed. University Science Books:
Sausalito, 1997.


 + xN
+ xN
 + |xN − x|
+ |xN − x| , N.
, N.  , N.
, N. 

 The average deviation is:
The average deviation is: 






















 *The relative uncertainty is given by the approximate formula:
*The relative uncertainty is given by the approximate formula: