Figure 3-6 shows the angular diameter of an object, its linear diameter, and its distance. Linear diameter is the distance between an object’s opposite sides. The linear diameter of the moon, for instance, is 3476 km. Recall that the angular diameter of an object is the angle formed by two lines extending from opposite sides of the object and meeting at your eye. Clearly, the farther away an object is, the smaller its angular diameter. The small-angle formula allows you to find any of these three quantities if you know the other two.

In the small-angle formula, you always express angular diameter in seconds of arc, and you always use the same units for distance and linear diameter:

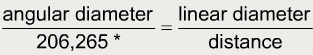
Example: The moon has a linear diameter of 3476 km and is about 384,000 km away. What is its angular diameter? Solution: You can leave linear diameter and distance in kilometers and find the angular diameter in seconds of arc:

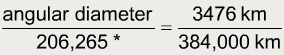
The angular diameter is 1870 seconds, which equals 31 minutes, of arc—about 0.5°.

*The number 206,265 is the number of seconds of arc in a radian. When you divide by 206,265, you convert the angle from seconds of arc into radians.