Force and Acceleration in Circular Motion

Introduction

Acceleration is the time rate of change of velocity. Since velocity is a vector, it can change in two ways: its magnitude can change and its direction can change. Either change gives rise to an acceleration. For circular motion at constant speed, the velocity is always tangential to the circular path, and therefore its direction is continuously changing even though its magnitude is constant. Therefore, the object has an acceleration. It can be shown that the magnitude of the acceleration a_c for uniform circular motion with speed v in a path of radius R is

a_c =

v²

and that the direction of the acceleration is inward toward the center of the circular path. This is illustrated in Figure 1.

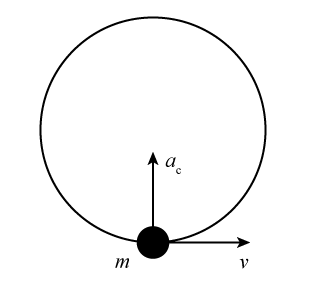
an image of a ball labeled m moving in a circular motion with a line a c pointing toward the middle of the circle and a line v pointing straight out perpendicular to the first line

Figure 1

Newton's second law requires that there be a net force on the object equal in magnitude to ma_c and in the direction of a_c. Circular motion with speed v in a path of radius R has period (time for one revolution) T and frequency (revolutions/s)

f = 1/T.

Since the object travels a distance 2πR (the circumference of its circular path) in time T the speed v is equal to

v =

2πR

= 2πRf

and

a_c = 4π²f ²R.

The setup for the experiment is shown in Figure 2. When the plastic tube is moved in a small circle above your head, the racketball moves around in a horizontal circle at the end of a string that passes through the tube and has a mass hanger with slotted masses suspended from its lower end. Applying

ΣF = ma

to the stationary mass hanger gives

F_string = Mg,

where F_string is the tension in the string and M is the sum of the masses of the mass hanger and the slotted masses that are placed on it.

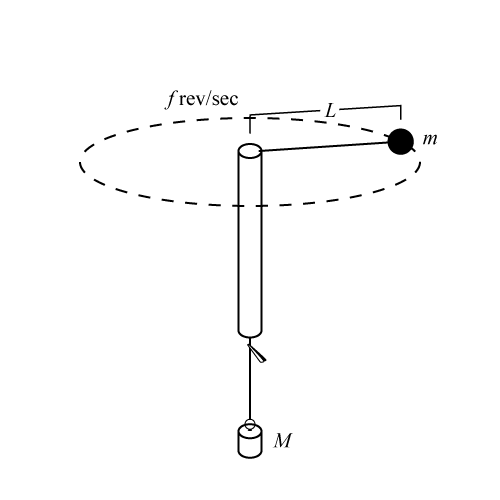
an image of a plastic tube with a string running through the middle. On the bottom of the string is a hanger labeled M and on the top of the string is a ball moving in a circular path around the top of the tube. The radius of the circular path is labeled L and the circle is label f rev / sec

Figure 2: Experimental setup

Because of the downward force of gravity on the ball, when the ball moves in a horizontal circle the string is at an angle θ below the horizontal, as shown in Figure 3. In the figure, L is the length of the string, measured from the center of the tube to the center of the ball. The radius R of the circular path of the ball is given by

R = L cos θ.

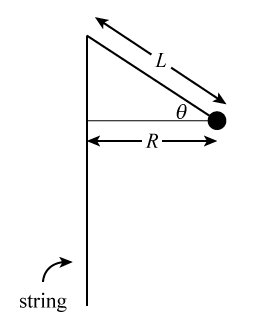
an image of a string bent into two segments. The first segment is vertical and labeled string. The second segment is bent at an angle theta below the horizontal and labeled L with the ball attached to its end. The distance from the ball to the vertical first segment is labeled R

Figure 3

The forces on the ball are gravity and the tension in the string. The tension in the string is directed along the string and the gravity force is straight downward. The free-body diagram for the moving ball is given in Figure 4. Since the ball moves in a horizontal circle, its acceleration is horizontal. It is convenient therefore to use coordinates that are horizontal and vertical, and in the force diagram F_string has been resolved into its horizontal and vertical components.

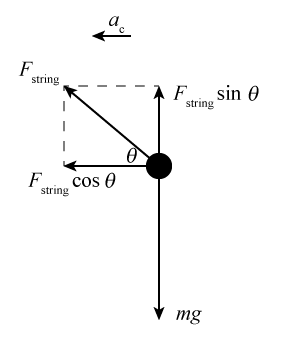
A free body diagram of the ball has a vector m g pointing down and a vector F string pointing to the left at an angle of theta above the horizontal. The components of F string are shown. F string sin theta points up and F string cos theta points to the left. Above the diagram is a vector a c pointing left.

Figure 4

ΣF_x = ma_x

gives

F_string cos θ = ma_c = m4π²f ²R.

R = L cos θ

F_string = m4π²f ²L.

And, since

F_string = Mg,

then

Mg = m4π²f ²L.

Rearranging gives the following equation.

f ² =

4π²m

Objective

In this experiment we will test the expression for the acceleration of an object moving in uniform circular motion.

Apparatus

Racketball with string and alligator clip attached
Plastic tube
Slotted mass set and hanger
Balance
Stopwatch
Meterstick

Discussion

As discussed in the Introduction for this experiment, application of Newton's second law in the experimental setup yields the following.

( 1 )

f ² =

4π²m

In this equation, f is the frequency of the circular motion of the ball and m is the mass of the ball. M is the mass suspended from the lower end of the string and L is the length of string between the center of the ball and the center of the upper end of the tube. Note that the angle θ that the string makes with the horizontal does not appear in Eq. (1). Derivation of Eq. (1) assumes that the acceleration of an object moving at constant speed v in a circular path of radius R has magnitude

a_c =

v²

and direction that is radially inward toward the center of the circular path. In this experiment, we will measure f for several values of M and L. We will use this data to test Eq. (1), and thereby to test the expression for a_c and our application of

ΣF = ma.

We will do this by plotting f ² versus

and seeing if our data is well-represented by a straight line that has zero y-intercepts. We will also use the slope of the line and a measurement of the mass m of the rotating object to calculate g and see how well the value obtained this way agrees with the actual value of g.

Procedure

Please print the worksheet for this lab. You will need this sheet to record your data.

For practice, place a slotted mass of 100 grams on the mass hanger at the lower end of the string and whirl the racketball over your head while holding onto the string below the tube. Practice spinning the ball over your head while maintaining the path of the ball completely horizontal, until you can let go of the string below the tube and maintain the same motion while the mass does not rise or fall. Each lab partner should do this exercise.

Pull enough string through the tube so the length L is 50.0 cm. Recall that L is the distance from the center of the top of the tube to the center of the ball. Attach an alligator clip to the string about 1 cm below the plastic tube to serve as a marker so you can keep L constant while whirling the ball. As you whirl the ball in a horizontal circle, make sure that the string or alligator clip does not come in contact with your hand or arm. Ensure that the ball is rotating in a horizontal circle before measuring the time. Then have your lab partner measure the time t₂₀₍₁₎ it takes for the ball to complete 20 revolutions. Interchange roles of whirler and timer and repeat the measurement to obtain time t₂₀₍₂₎. Repeat taking measurements until you get a pair of times that differ by less than 2.0 seconds.

Enter your values of t₂₀₍₁₎ and t₂₀₍₂₎ into the column for

M = 150 grams

in Table 1. Note that

f₁ =

t₂₀₍₁₎

f₂ =

t₂₀₍₂₎

and let

f =

f₁ + f₂

Complete the rest of the column. Repeat the procedure for the other sets of M and L values. Remember that M is the total mass suspended from the string, the mass of the hanger plus the mass of the slotted masses placed on the hanger.

Open Excel and plot f ² (for f in rev/s) versus

in kg/m. Use Excel to find the equation for the straight line that is the best fit to your data. All your data points should fall close to this line and the y-intercept of the line should be close to zero. If one, or both, of these isn't the case, you have made a mistake in collecting, recording or graphing your data. If you and your lab partner can't find what is wrong, ask your TA for help.

Record the slope of the line that is the best fit to your data.

Use the balance to measure the mass of the ball. Record your results.

Use Eq. (1), the slope you recorded, and the mass of the ball to calculate g.

If the actual value of g is taken to be 9.80 m/s², what is the percentage difference between your experimental result and the actual value of g? In the calculation retain enough significant figures to avoid round-off error.