Simple Harmonic Motion

Objective

•
to define the characteristics that change the period of oscillation for a mass-spring system
•
to measure the dynamic spring constant of a spring-mass system
•
to test the law of conservation of energy

Equipment

collision cart of a known mass on a horizontal dynamics track oscillating by the means of springs in parallel, motion sensor and photogate connected to the Science Workshop Interface, nonlinear springy objects (rubber bands), two rectangular weights of ~0.5 kg each to change the mass of the system

Figure 1

Introduction and Theory

Simple Harmonic Motion

If the hanging mass is displaced from the equilibrium position and released, then simple harmonic motion (SHM) will occur. SHM means that position changes with a sinusoidal dependence on time.

( 1 )

x = X_max cos(ωt)

The following are the equations for velocity and acceleration.

( 2 )

v = −X_maxω sin(ωt)

( 3 )

a = −X_maxω² cos(ωt)

By substituting equation 1, equation 3, and Hooke's Law (F_el = –kΔx) into Newton's Second Law, one can derive the equation for the angular resonant frequency of the oscillating system:

( 4 )

ω =

where k is the spring constant and m the mass of the system undergoing the simple harmonic motion. The unit of angular frequency is radians per second (rad/s). The natural resonant frequency of the oscillator can be changed by changing either the spring constant or the oscillating mass. Using a stiffer spring would increase the frequency of the oscillating system. Adding mass to the system would decrease its resonant frequency. Two other important characteristics of the oscillation system are period T and linear frequency f. The period of the oscillations is the time it takes an object to complete one oscillation. Linear frequency is the number of oscillations per second. The period is inversely proportional to the linear frequency.

( 5 )

T =

The unit of the period is a second (s) and the unit of the frequency is Hertz, or s^–1 (Hz = 1/s). The angular frequency is related to the period and linear frequency according to the following expression.

( 6 )

ω = 2πf =

2π

From equations 5 and 7, it follows that the period of oscillations can be found as

( 7 )

T = 2π ·

Energy

In order for the oscillation to occur, the energy has to be transferred into the system. When an object gets displaced out of equilibrium, then elastic potential energy is being stored in the system. After the object is released, the potential energy transforms into kinetic energy and back. In the harmonic oscillator, there is a continuous swapping back and forth between potential and kinetic energy. For an oscillating spring, its potential energy E_p at any instant of time equals the work W done in stretching the spring to a corresponding displacement x.

( 8 )

E_p = W =

kx²

The kinetic energy E_k of the oscillator for any instance of time will follow the well known equation

( 9 )

E_k =

mv².

The maximum potential energy and maximum kinetic energy can be calculated accordingly.

( 10 )

E_p =

kX_max²

( 11 )

E_k =

mV_max²

According to the law of conservation of energy: "The mechanical energy is conserved (neither destroyed nor created) in the frictionless oscillating system."

Procedure

Please print the worksheet for this lab. Answer all the questions on the Lab Worksheet prior to submitting the Inlab in WebAssign.

Checkpoint:
Be sure to have your TA sign your lab worksheet, printed Inlab, and all printed graphs after each part is completed. Be sure the data can be seen on the graphs.

In this experiment, you will verify if the period depends on the amplitude, and calculate the resonance frequency and spring constant of a system. You will record the collected data in the WebAssign Inlab.

Part 1: Period vs. Amplitude

Setup the experiment as shown in Figs. 2 and 3. Open the preset experiment file: desktop\pirt inst labs\PHY 113\PreSet Up Labs\SHM.

Figure 2

Figure 3

With no added mass, measure the period of oscillations for starting amplitudes of 4 cm and 12 cm. Data acquisition will stop automatically after 5 sec. The sample recording is shown in Fig. 4. The period is measured by the photogate and recorded in the table to the left of the graph.

With no added mass, displace the cart from its equilibrium position by about 8 cm and start the recording. Record again the period of oscillations of a cart measured by the photogate. Record all three periods of oscillations in the Inlab.

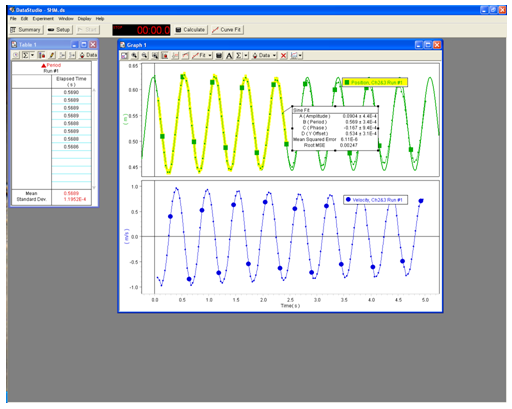
Figure 4: A sample file for SHM experiment in DataStudio

Part 2: Conservation of Energy

Fit the recording of position vs. time to the sine wave. Parameter A is amplitude (maximum displacement) of the oscillations. Parameter B gives you the period of oscillations. You can compare its value to the value of the period measured by the photogate. Parameter D is the equilibrium position. Record these parameters in the Inlab.

Fit the recording of the velocity vs. time to the sine wave. Record parameter A—the amplitude (maximum value) of the velocity vs. time graph—in the Inlab.

Notice that both graphs, position vs. time and velocity vs. time, are periodic waves of the same frequency shifted by 90°, or

rad.

The maximum and minimum values of the position occur when the velocity is zero, and likewise the maximum and minimum values of velocity happen when the position is at its equilibrium. In terms of the energy of the system, it means that when the potential energy is a maximum (maximum displacement), the kinetic energy is zero. At this moment, energy is all potential. Likewise at the point when the spring is not stretched (the object passes an equilibrium point), the energy is all kinetic. To verify the conservation of energy theorem for the oscillating cart, it is sufficient to compare its maximum potential energy with its maximum kinetic energy by finding the percent difference of the energy loss.

( 12 )

%loss =

PE_i − KE_f

PE_i

· 100%

Part 3

3a. Measure the Spring Constant

Use parameter B to calculate the resonance frequency and spring constant of a system using equations 6

ω = 2πf =

2π

and 4

ω =

from the Introduction and Theory section of this lab manual.

3b. Relationship Between Period and Mass This is the part of the experiment where you will verify that the period of the SHM is proportional to the square root of the mass.

Load the cart with heavy masses (one at a time) and measure the period of SHM while keeping the amplitude constant (e.g., 8 cm).

Including the data from the previous part of the experiment, you will have three points to make a graph of period

vs.

According to the theory (equations 4

ω =

and 6

ω = 2πf =

2π

), this graph should be a straight line.

Record the slope of the

T vs.

graph in the Inlab.

Use the value of slope and its uncertainty to find the spring constant.

Based on the slope of the graph, calculate the dynamic spring constant of the system.

Hint: Substituting

ω =
2π
T

into

ω =
k
m

gives

2π
T
=
k
m
.

Solving for T yields the following.

T =
2π
k
m