Print

LR, LC, and LRC Circuits

Introduction

In this lab you will be investigating the transient behavior of circuits containing inductors. By transient behavior we are referring to what happens in a circuit when the power is either turned on or off suddenly.

LR Circuits

We start by reminding ourselves of the voltage across a resistor (R), a capacitor (C) and an inductor (L).
( 1 )
VR = IR
( 2 )
VC =
q
C
( 3 )
VL =
dI
dt
L
Further, we have defined the current flowing in a circuit in terms of the rate of charge passing a point in the circuit as
( 4 )
I =
dq
dt
.
Combining these four relationships, we can rewrite the value of the voltage across each of these circuit elements in terms of the charge as
( 5 )
VR =
dq
dt
R;    VC =
q
C
;    VL =
d2q
dt2
L.
In an earlier lab, we have already investigated what happens when we charge and discharge a capacitor, so here we will use the same approach to investigate the behavior of a circuit containing an inductor when we turn on and off the power to the circuit.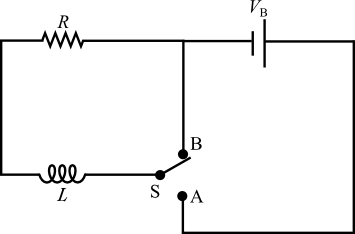
A circuit diagram with a battery on the top labled V_B. The positive side of the battery goes to node A where there is a switch. The negative side of the battery goes to a fork where one wire runs to node B where the switch is. The other wire goes through a resistor labled R then an inductor labled L and ends at node S where the switch is. The switch is in a position connecting nodes B and S. It can be flipped to instead connect nodes A and S.
Figure 1
Consider the circuit shown in Figure 1, where initially the switch is in position B and there is no current flowing in the series LR circuit. Suppose now that we move the switch to position A allowing current to begin flowing in this circuit. We know from our discussion of circuits in class that
( 6 )
VB = VR + VL = IR +
dI
dT
L,
where the solution for I(t) can be found as we did in the case of RC circuits previously by integrating this equation with respect to time. We then find that
I(t) =
VB
R
1 − e−(R/L)t
,
where the quantity L/R has dimensions of time and is called the "time constant" for this circuit (τL)
τL =
L
R
.
We can plot the solution for I(t) and its derivative below and see that they both have an exponential behavior with a time constant τL.
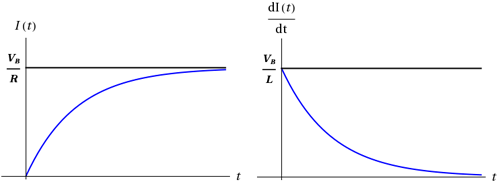
There are two figures here. On the left side, a coordinate plane has the horizontal axis labeled t and the vertical axis labeled I(t). A concave down and increasing curve starts at the origin and reaches the maximum value I(t) = V_B/R asymptotically as t approaches infinity. On the right side, a coordinate plane has the horizontal axis labeled t and the vertical axis labeled dI(t)/dt. A curve starts at the maximum value dI(t)/dt = V_B/L at t = 0 and decays exponentially, reaching the minimum value dI(t)/dt = 0 asymptotically as t approaches infinity.
Figure 2
After a long period of time, the current in the circuit will reach the "steady state" value of
VB
R
 as shown in the figure above. Also at this same time, the derivative of the current with respect to time is approaching zero and hence the voltage drop across the inductor
VL = L
dI
dt
 in this circuit approaches zero. Suppose at this time, we now move the switch from position A back to position B. In this configuration, we have removed the power source from the RL circuit and the inductor will now "drain" through the resistor. With the battery removed, we can now rewrite Equation (6)
VB = VR + VL = IR +
dI
dT
L,
 to get the following.
0 = VR + VL = IR +
dI
dt
L
Solving again for I(t) using
τL =
L
R
 we find
( 7 )
I(t) = Ioe−t/τL.
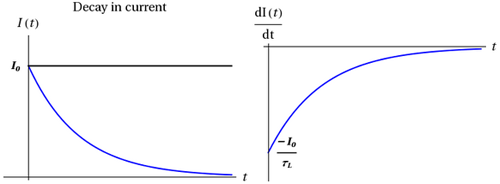
There are two figures here. On the left side, a coordinate plane has the horizontal axis labeled t and the vertical axis labeled I(t). Above the graph it says Decay in current. A curve starts at the maximum value I(t) = I_0 at t = 0 and decays exponentially, reaching the minimum value I(t) = 0 asymptotically as t approaches infinity. On the right side, a coordinate plane has the horizontal axis labeled t and the vertical axis labeled dI(t)/dt. A concave down and increasing curve starts at dI(t)/dt = -I_0/tau_L and reaches the maximum value of 0 asymptotically as t approaches infinity.
Figure 3
We can investigate the voltage across the inductor in this circuit during the rising and falling of the current in the two circuits just analyzed. Since we know that
VL =
dI
dt
L and τL =
L
R
,
we can quickly write down the voltage in these two cases from the solutions that we found for I(t) earlier.
"current rising"    
VL = VB e−t/τL
 "current falling"    
VL =
−Io
τL
e−t/τL
 L =
−Io
R
L
e−t/τL
 L = −VB e−t/τL
Notice that the two solutions for the current have the same time dependence but with a maximum starting value that is opposite in sign.
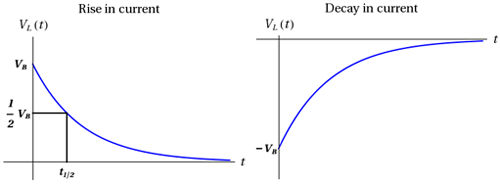
There are two figures here. On the left side, a coordinate plane has the horizontal axis labeled t and the vertical axis labeled V_L(t). Above the graph it says Rise in current. A curve starts at the maximum value V_L(t) = V_B at t = 0 and decays exponentially, reaching the minimum value V_L(t) = 0 asymptotically as t approaches infinity. A horizontal and vertical line starting at the y and x axis respectively meet at a common point on the curve. At the y axis the horizontal line is labled 1/2 V_B. At the x axis the vertical line is labled t_1/2. On the right side, a coordinate plane has the horizontal axis labeled t and the vertical axis labeled V_L(t). Above the graph it says Decay in current. A concave down and increasing curve starts at V_L(t) = -V_B and reaches the maximum value of 0 asymptotically as t approaches infinity.
Figure 4
As we did in the case of the RC circuits previously, we can define a quantity called the "half-life" t1/2 as the time it takes for the voltage to reach half of its original value (it is easier to estimate a point on the curve at half the maximum value than at 1/e of the maximum value).
( 8 )
t1/2 = τL ln(2)

LC Circuits

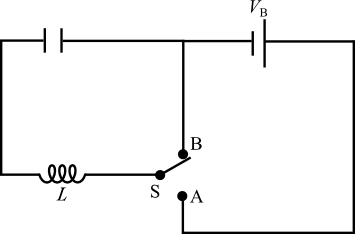
A circuit diagram with a battery on the top labled V_B. The positive side of the battery goes to node A where there is a switch. The negative side of the battery goes to a fork where one wire runs to node B where the switch is. The other wire goes through a capacitor then an inductor labled L and ends at node S where the switch is. The switch is in a position connecting nodes B and S. It can be flipped to instead connect nodes A and S.
Figure 5
Next we are going to investigate the circuit that contains just an inductor and a capacitor and see what type of behavior this circuit exhibits. From our study of this type of circuit in the text, you may already suspect that this circuit will exhibit electrical oscillations. Let's begin by considering the circuit shown in Figure 5. Here we have connected a capacitor and an inductor into a loop. From Equations (1)
VR = IR
, (2)
VC =
q
C
, and (3)
VL =
dI
dt
L
 above, we know that the voltage across the capacitor is related to the voltage across the inductor as follows.
VC =
q
C
 = VL = −L
dI
dt
If we write this relationship in terms of the charge on the capacitor and its derivatives we find that
q
C
 = −L
d2q
dt2
or rewriting this we find
( 9 )
q
C
 + L
d2q
dt2
 = 0
which is the familiar equation that describes a system undergoing simple harmonic motion. Given that we have solved this equation for x(t) in the case of harmonic oscillations, and we know that
( 10 )
x(t) = A cos(ωt + φ),
we can then use this solution to write down the form of the solution for the charge in the circuit as a function of time as just
( 11 )
q(t) = Q cos(ωt + φ)
where the angular frequency, ω, in the solution is related to the L and C in the circuit as
( 12 )
ω =
1
LC
.
These simple electrical oscillator circuits have been used to create oscillating voltages and currents in a wide variety of circuit application for many decades, but more recently they have been replaced by the cheaper, more reliable and more accurate crystal oscillator circuits since the internal resistance of the system causes these oscillations to gradually die off in time. If we account for this loss due to the internal resistance of the inductor/capacitor combination we then get a series RLC circuit where the total potential at any instant of time must satisfy
( 13 )
Vtotal = VC + VR + VL =
q
C
 + R
dq
dt
 + L
d2q
dt2
.
The solution for this differential equation is just like that found for harmonic oscillation with damping back in mechanics. From those solutions we found
q(t) = Ae−(R/2L)t cos(ω' t)
with
( 14 )
ω' =
1
LC
 −
R2
4L2
.
We will be investigating these solutions in more detail in the lab which follows.

Objective

In this lab you will build an RL and an LC circuit and use the response of these circuits to a time varying voltage that we calculated above to measure the value of the inductance (LR circuit) and the frequency of oscillation of the LC circuit. You will also investigate the effect of the internal resistance in the LC circuit and how that modifies the solution for the charge as a function of time in these circuits.

Apparatus

  • Oscilloscope
  • Function generator
  • 0-40 volt power supply
  • Circuit box
  • Multimeter
  • Miscellaneous banana lead wires
The required apparatus, an oscilloscope, a function generator, a power supply, a multimeter and a circuit box.
Figure 6: Equipment
The front panel of a function generator.
Figure 7: Function Generator
Caution:
Please, be careful in handling all of the equipment in this laboratory. The equipment is expensive and can be easily damaged if misused.
The front panel of an oscilloscope.
Figure 8: Oscilloscope

Procedure

Please print the worksheet for this lab. You will need this sheet to record your data.

PDF file

Setting Up the Oscilloscope

1
Begin by locating the ON/OFF button on top of the oscilloscope. Press this button. The front screen should light up. The oscilloscope will then conduct a self-test to verify the instrument is operating correctly. Wait for the confirmation that everything is OK before proceeding.
It is always a good idea to check the settings of an oscilloscope before beginning any measurements. The following is the set-up procedure to prepare the oscilloscope for the measurements in this laboratory experiment. Most of these settings are probably already preset. Just verify the settings to be sure. The oscilloscope will always reset to the previous settings (the settings that were on the oscilloscope when it was turned off).
2
Check oscilloscope settings.
  • a
    Press the DISPLAY button. The settings (shown on the right edge of the screen) should be the following.
    • •
      Type [Vectors]
    • •
      Persist [Off]
    • •
      Format [YT]
    • •
      Contrast Increase (Adjustable as needed)
    • •
      Contrast Decrease (Adjustable as needed)
      • •
        NOTE: If the intensity is OK, skip this step.
  • b
    Press the TRIGGER MENU button. On the right side of the oscilloscope screen, there are five sections controlled by the five buttons to the right of these sections.
    • •
      Video [Edge]
    • •
      Slope [rising]
    • •
      Source [CH 1]
    • •
      Mode [Auto]
    • •
      Coupling [DC]
    If the settings are not preset to these values, press (once) the button located to the right of the section, next to the scope screen.
  • c
    Press the CH 1 MENU button. The four sections (in the same location as the five sections in part a above, should be set to the following.
    • •
      Coupling [DC]
    • •
      BW Limit [OFF]
    • •
      Volts/Div [Coarse]
    • •
      Probe [1x]
  • d
    Press the HORIZONTAL MENU button. The following are the sections that should be selected.
    • •
      [Main]
    • •
      Trig knob [Level]
  • e
    Press the MEASURE button. The five sections should be set to the following.
    • •
      Source [Type]
    • •
      CH 1 [Freq]
    • •
      CH 1 [Period]
    • •
      CH 1 [Pk - Pk]
    • •
      CH 1 [Cyc RMS]
  • f
    Locate the VOLTS/DIV knob for CH 1 and adjust it until 2.00 V is displayed on the lower left of the oscilloscope screen.
  • g
    The MEASURE DISPLAY mode should remain on your screen while performing all of your measurements.
3
You are now ready to make measurements on your circuit.

Setting Up the Function Generator

1
You will now use a function generator to produce a signal on the oscilloscope. In order to prepare the generator for use, preset the control as follows.
  • a
    Press the POWER button (orange button on the lower left side).
  • b
    Press the [1k] button on the top row of green buttons.
  • c
    Press the [square wave] button on the second row of green buttons.
  • d
    Adjust the FREQUENCY control until a reading of 1.500 is displayed on the generator digital readout.
  • e
    The MOD ON and MOD EXT lights should be off.
  • f
    Rotate the AMPL knob clockwise about 1/2 turn. This should produce an output of about 10 volts.
2
The oscilloscope volts/div and sec/div settings should be:
  • VOLTS/DIV    2.00 V
  • SEC/DIV    250 microsec (This setting may be checked by looking at the bottom of the screen [after the symbol M].)
Using the two BNC-banana cables connect the OUTPUT of the function generator to CH 1 of the oscilloscope. Adjust the AMPL(itude) control of the function generator in order to display a 2-3 division waveform on the screen. Note as you adjust the AMPL, the section on the right side (Pk-Pk) of the oscilloscope is reading the Peak to Peak voltage of the waveform on the screen.

Measuring the Transient Behavior of a Simple RL Circuit

The objective of this experiment is to observe and measure the transient response of a series resistor-inductor RL circuit. You will also see how to use this to measure and determine the inductance in such a circuit.
1
The basic unit of inductance is henry, which is defined as the inductance necessary to produce 1 volt of EMF for a current change of 1 A/s through the device. The most commonly used units are mH
(1 mH = 10−3 H).
 The inductor which you will probably use will be marked with an approximate value of its inductance in mH.
A circuit diagram showing a function generator on the right side. The top wire of the function generator goes through a 150 ohm resistor labeled R_1, a 0.1 micro farad capacitor labeled C_1. Then the wire comes to a fork with one leg going to ground and the other returning to the bottom of the function generator. On the left there is a circle labeled Scope with arrows coming from the top and bottom pointing to above and below the capacitor indicating where the oscilloscope leads should be attached. A wire with a ground symbol at the end indicates that the scope is also connected to ground.
Figure 9

Finding the Value of the Inductance

2
Connect the circuit as shown in Figure 9.
3
Set the frequency of the function generator to 1 KHz (square wave), and the amplitude to maximum.
4
Set the oscilloscope as described in the Setting Up the Oscilloscope section of this experiment.
5
Connect CH 1 input of the oscilloscope across the inductor (L) in the circuit as shown. Rotate the knobs on the oscilloscope to display the decaying voltage on the inductor such that the trace touches the top line of the screen and decays to the bottom line of the screen. The trace does not have to fill the screen (horizontally), but it does have to extend over at least 4–5 divisions in order to measure the decay constant. (See Figure 10.)
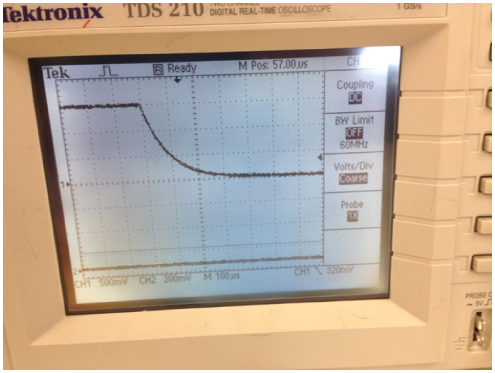
The screen on an oscilloscope. It shows one signal on the top going horizontally for the first three of ten horizontal divisions of the graph, then decreasing exponentially and asymtotically reaching a value of 1. Visually the graph reaches 1 in four horizontal divisions from the beginning of the curve. The second signal is at 2 across the whole graph. On the sides of the graph the following is indicated. M Pos: 57.00 micro seconds, Coupling DC, BW Limit OFF 60 MHz, Volts/Div Coarse, Probe 1X, CH1 500 mV, CH2 200 mV, M 100 micro seconds, CH1 320 mV.
Figure 10
6
Record the voltage value of this waveform for at least 10 evenly spaced time intervals from the peak of the wave through its decay to the baseline and record these readings, in Table 1, as a time and voltage for each reading.
7
Using this data, record in Table 1 the time and the ln(Voltage).
8
Plot this as a scatter plot using Excel. Using the trendline feature in Excel, fit this curve with linear function and find the slope and intercept of this curve.
9
How are these two quantities related to the Imax, R and L of this circuit as described in Equation (7)
I(t) = Ioe−t/τL.
?
10
Disconnect the resistor (R) from the circuit and measure its resistance. (Note that the internal resistance of the function generator is 50 ohms.)
11
Calculate the experimental value of the inductor (L) in the circuit using the formula
τ =
L
R
,
 where R is the TOTAL resistance in the circuit. Call it (experimental) L1. Do not forget the units.
12
The component value of the inductor is written on the component "bread board". Read and record this value as L2.
13
What is the percent error between the experimental value and the component value of the inductor? Which value do you consider to be more accurate? Why?

Measuring the Oscillatory Behavior of a Simple LC Circuit

1
The objective of this experiment is to observe and measure the transient response of a series inductor-capacitor, LC circuit.
2
Connect your inductor and capacitor into the circuit configuration shown in Figure 11.
A circuit diagram showing a function generator on the right side. The top wire of the function generator goes through an inductor laebled L and a 0.1 micro farad capacitor labeled C_1. Then the wire comes to a fork with one leg going to ground and the other returning to the bottom of the function generator. On the right there is a circle labeled Scope with arrows coming from the top and bottom pointing to above and below the capacitor indicating where the oscilloscope leads should be attached. A wire with a ground symbol at the end indicates that the scope is also connected to ground.
Figure 11
3
Set the frequency of the function generator to 1 KHz (square wave), and the amplitude to maximum.
4
Set the oscilloscope as described in the Setting Up the Oscilloscope section of this experiment.
5
Connect CH 1 input of the oscilloscope across the capacitor (C) in the circuit as shown. Rotate the knobs on the oscilloscope to display the oscillating voltage on the capacitor such that the trace is centered on the screen. Since for this part of the experiment, you wish to measure the frequency of these oscillations, you will need to adjust the sweep speed to allow you to measure the time between cycles of this oscillation. Note that these oscillations gradually decay away to zero if we wait long enough. (See Figure 12.)
6
Record the voltage value for the peaks of these oscillations for at least 5 of these peaks and record these readings in Table 2. Record these readings as a time and voltage for each reading.
7
Using this data, record in Table 2 the time and the ln(Voltage).
8
Plot this as a scatter plot using Excel. Using the trendline feature in Excel, fit this curve with linear function and find the slope and intercept of this curve.
9
How are these two quantities related to the Qmax, RC of a series RC circuit? What is the value of R that you find that matches this decay time? (This decay is caused by the internal resistance of the capacitor and the inductor in the circuit.)
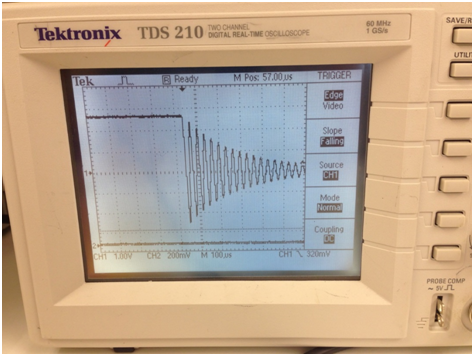
The screen on an oscilloscope. It shows one signal on the top going horizontally for the first four of ten horizontal divisions of the graph, then oscillating about 1 with a deceasing amplitude. The second signal is at 2 across the whole graph. On the sides of the graph the following is indicated. M Pos: 57.00 micro seconds, TRIGGER, Edge Video, Slope Falling, Source CH1, Mode Normal, Coupling DC, CH1 1.00 V, CH2 200 mV, M 100 micro seconds, CH1 320 mV.
Figure 12
10
Now take this same data and measure the time intervals between successive peaks. Use this data to find the average value of the period of these oscillations.
11
How does this period compare to the period that we expect from an LC circuit according to Equation (14)
ω' =
1
LC
 −
R2
4L2
.
 based on your measurement of the inductance of the inductor earlier in this lab?
12
What is the percent error between the experimental value and the component value of the inductor? Which value do you consider to be more accurate? Why?

Copyright © 2013-2014 Advanced Instructional Systems Inc. and Texas A&M University. Portions from North Carolina State University. | Credits