Waves on a String

introduction

Wave motion is the underlying principle for many common phenomena (sound, musical instruments, light, X-rays, etc.) and may be transverse or longitudinal in nature. For longitudinal waves, the displacement of each particle of the medium is parallel to the direction in which the wave propagates. In transverse wave motion, the displacement of the particles is perpendicular to the direction of the wave propagation. The characteristics of transverse waves can be studied using standing waves on a stretched string. Standing waves (for both longitudinal and transverse wave motion) are extremely important since many bodies vibrate with standing waves. In this experiment, the relationship between the tension in a string and the vibrational frequencies of a standing wave pattern will be examined.

Theory of the Wave Equation

Suppose a string with a linear mass density (mass per unit length) of ρ is fixed at both ends and is placed under a tension T. The vertical displacement, y, of every point along the string is described by the wave equation

( 1 )

∂² y

∂ x²

= ρ

∂² y

∂ x²

where x is the horizontal position of some point on the string (you should see your text for the derivation of this expression). When waves propagate along the string (in the x-direction), each particle in the string moves at right angles to the string's original undisturbed position. The wavelength, l, is the length of one complete cycle, from a point on the wave to the next point on the wave which is in the same phase (or more simply, the distance between two successive crests or two successive troughs). The period, τ, is the time required for a crest (or trough) to travel one wavelength. The frequency, f, is the number of waves that pass a given point in a given time and it is related to the period by

τ =

Wave Speed

For any transverse wave on a string, the speed of the wave is given by

( 2 )

v = λf.

A string of length, L, experiencing a tension, can be made to vibrate in many different modes. When the tension, the frequency of vibration and the length of the string are properly related, standing waves can be produced. For a string with a tension, T, the velocity of the waves is given by

( 3 )

v =

Standing Waves

Of the many solutions to the wave equation, one of particular interest is the solution for standing waves. Standing (or stationary) waves can be produced when two wave trains of the same wavelength, frequency, and amplitude travel in opposite directions through the same medium and interfere with each other. For a stretched, uniform string fixed at one end, a train of transverse waves traveling along the string will be reflected at the fixed end and interfere with the oncoming wave train. The amplitude, wavelength, and frequency do not change upon reflection and if the conditions are suitable, a standing wave pattern will result. A solution to the wave equation for standing waves is given by

( 4 )

y(x, t) = A sin(kx) cos(ωt)

where

( 5 )

k =

2π

, ω =

2π

When the string vibrates in a standing wave pattern, the points with no vertical vibration are called nodes; the points where the string has the largest vertical displacement are called antinodes. The distance between two nodes is a half wavelength. If the ends of the string are fixed in position, the ends will function as nodes and the string must vibrate in a whole number of segments. If the string has only one segment, the length, L, of the string is equal to

λ,

if it vibrates in two segments, L is equal to λ, if it vibrates in three segments then L equals

(see Figure 1).

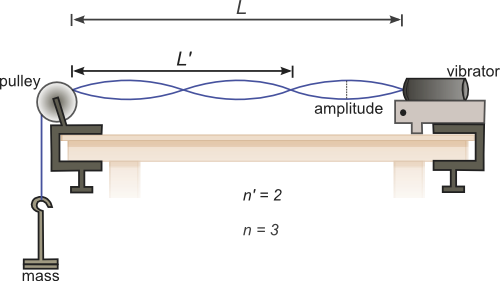
In this diagram, two clamps are affixed to the ends of a table. Atop one clamp is a pulley, and atop the other clamp is a vibrator. A string runs horizontally from the vibrator, along the length of the table to the pulley, and then hangs over the pulley. A mass holder tied to the hanging end of the string is held aloft in the air. The horizontal portion of string between the vibrator and pulley vibrates in a standing wave pattern. The horizontal distance between two nodes is labeled L prime. The horizontal distance between three nodes is labeled L. The vertical distance between the lowest and highest points of vibrations is labeled amplitude. Two relations are stated: n prime = 2 and n = 3.

Figure 1

Thus for any vibrational mode for a standing wave pattern on a string with fixed ends, the length of the string will be an integral number of half-wavelengths.

( 6 )

L =

If Equations (1), (2), and (3) are combined, the result is

( 7 )

ρ =

Tn²

4f²L²

When the tension in the string is produced by suspending a mass, M, from its end, the tension is then equal to the weight of the mass

T = Mg

and the density of the string is

( 8 )

ρ =

Mgn²

4f²L²

So the density of the string can be determined by measuring the tension of the string, the length of the segments and the frequency of vibration.

Objectives

The objectives of this lab are to investigate the relationships between the tension in the string, and the frequencies of vibration necessary to produce a "standing wave" on the string. From these measurements we will also be able to make a measurement of the linear mass density of the string being vibrated.

Apparatus

Electrically driven vibrator
Two uniform strings
Pulley
Mass holder
Set of slotted masses with small masses (5g (1ea), 2g (2ea), 1g (1ea)) in a plastic dish
Meterstick
Stroboscopic light

In this experimental setup, two clamps are affixed to the ends of a table. Atop one clamp is a pulley, and atop the other clamp is an electrically driven vibrator. A string runs horizontally from the vibrator, along the length of the table to the pulley, and then hangs over the pulley. A mass holder tied to the hanging end of the string is held aloft in the air. Also atop the table are a set of small slotted masses and a stroboscopic light.

Figure 2

Procedure

Please print the worksheet for this lab. You will need this sheet to record your data.

Apparatus and Standing Waves

One end of a uniform string is attached to a vibrator armature which produces waves along the string at a frequency of 120 vibrations per second. The string passes over a pulley, and a mass holder is attached to the opposite end. By varying the mass on the holder, the tension in the string can be adjusted to produce standing waves with different wavelengths.

Two things to keep in mind are:

i
Since one end of the string is attached to the motor, the segment (oval-shaped part of the string that consists of a node–antinode–node) connected to the motor must be neglected, because the motion at the motor prevents a true node from forming at that end. Therefore, whenever n segments are counted the last one, the one next to the motor (vibrator), is neglected. When the length, L, of the standing wave pattern is measured, the neglected segment adjacent to the motor is not included.
ii
Standing waves are a quantized phenomenon. The standing wave pattern appears only at precise values of M and disappears if M deviates by just a few grams. So, M must be adjusted with precision.

Data

Connect the vibrator to the 110-volt, 60-cycle outlet on the table. Take the thin black string that is fastened to the vibrator armature and pass it over the groove in the pulley. Measure and record the length of the string before you begin. Attach the mass holder to the string and increase the tension in the string by adding slotted masses to the holder until the string vibrates in a standing wave pattern. Adjust the mass on the string until it is vibrating in

n = 3

segments. Maximize the amplitude of the standing wave pattern by adding (or removing) small masses to the string.

Since the node nearest the vibrator is distorted, this node and the first segment adjacent to the vibrator will not be considered when taking measurements. Thus

will be the length of

n' = n − 1

segments. Record the value

n'.

Measure, to the nearest mm, the distance

between the first node beyond the vibrator and the point where the string contacts the pulley (see Figure 1). Record your data in Table 1.

Determine

ΔL',

the uncertainty in the length. For an ideal string a node would be an exact point; however in the case of real strings, a node is not clearly defined but is instead spread out over a small length. This spreading will be used as an estimate of the uncertainty of

L'.

Measure and record

ΔL',

the length of the node.

Place the meterstick behind the wave pattern to obtain a rough estimate of the maximum amplitude of an antinode. To obtain the uncertainty in the mass, add to (or remove from) the mass holder enough mass to decrease the amplitude of the antinode to one-half its original value. Record the change in the mass as

ΔM'.

Using the same string, adjust the tension in the string by altering the mass on the holder until the string vibrates in a pattern having

n = 4 (n' = 3)

segments. Repeat procedures 2-4 to obtain values for

M', ΔM', L' and ΔL'.

Using the same string, form a pattern with

n = 5

segments. Repeat procedures 2–4.

Repeat procedures 1–4 with the thick black string for

n = 2,

3, and 4 segments.

Turn the stroboscope on and observe the string when it is vibrating in a standing wave pattern. When the stroboscope is tuned to the same frequency with which the string is vibrating, the motion of the string appears to stop. Use the stroboscope to determine the frequency of the vibrating string.

Caution:
Do not allow the stroboscope to remain on for longer than 1 minute at a time.

Calculations

For each value of

in your table compute the density (and uncertainty) for the thin black string using Equation (8).

Find the percent error between the standard value of the density of string (given by the lab instructor) and each of your calculated values.

For each value of

n',

use Equation (8) to compute the density (and uncertainty) of the thick black string.

Find the percent error between the standard value and each of your calculated values for the thick black string.

Using the standard density for the thin black string along with Equation (6) and Equation (8), calculate the wavelength, λ, when the string vibrates with n = 6, 7, and 8 segments. (For these calculations, assume that the distortion for the portion of the wave nearest the source of vibration can be neglected so that you can use the full length of the string for these calculations.) See Data step 6. What mass should be placed at the end of the string for each of these cases?

Questions

Can standing waves be produced along a string that is clamped at irregular intervals? Explain.

When standing waves are produced on the string by the vibrator, the string vibrates with the same frequency as the vibrator and a resonance is said to exist between the two. If the system is in resonance when the string vibrates in two segments, will the condition for resonance still exist if the mass on the string is increased by a factor of two? By a factor of 4? Explain.

Stringed instruments such as the piano, guitar, and violin produce sound when the strings vibrate in standing waves. What properties of waves affect the

a
pitch,
b
loudness, and
c
purity of the musical note produced?