The Tangent Galvanometer

Purpose

•
To investigate the magnetic field at the center of a current-carrying loop of wire.
•
To verify the right-hand rule for the field inside such a current loop.
•
To investigate the vector nature of magnetic fields and gain some experience with the way they add vectorially.
•
To verify the relationship between the current, I, the number of turns, N, and the magnetic field, B, inside a current loop using Earth's field as a reference.
•
To determine the strength of Earth's magnetic field at the lab's virtual location. (This is probably not your actual location. If it is, please send me a postcard.)
•
To verify your results using NOAA's National Centers for Environmental Information.

Equipment

Virtual Tangent Galvanometer
VPL Grapher
Pencil

Simulation and Tools

Open the Tangent Galvanometer simulation to do this lab. You will need to use the VPL Grapher to complete this lab.

Theory

You've learned that the magnetic field due to the current at a point in a straight wire takes on a circular shape around the wire (Figure (1a)). You've further found that by wrapping a length of wire into a loop, the field on one side of the wire can be "focused" into the small area inside the loop, resulting in an area of stronger magnetic field (Figures (1b) and (1c)).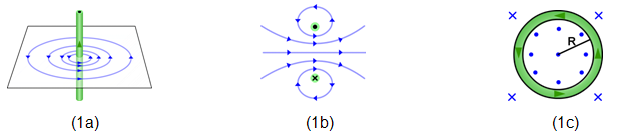

Figure 1: Magnetic Field Produced by a Current: (a) Straight wire's field (b) Loop's field viewed edge-on (c) Loop's field viewed face-on

The directions of the magnetic fields produced in Figures (1a) and (1c) can be remembered by the use of a pair of right-hand rules. (Wording and numbering vary depending on the source.) Note that, as usual, "current" refers to a conventional current, which is a flow of positive charges.

The Right-Hand Rule for the Field Around a Current-Carrying Wire:

If you grasp the wire in Figure (1a) with your right hand so that your fingers are wrapped around the wire and your thumb points in the direction of the current, the tips of your fingers will point in the direction of the field around the wire.

The field due to a current loop is shown in Figures (1b) and (1c). The direction of the field can actually be found from the first rule, but it's handy to create a second rule given how often we'll work with fields produced by current loops and solenoids.

The Right-Hand Rule for the Field Inside a Current-Carrying Loop of Wire:

If you grasp the loop in Figure (1c) with your right hand so that your fingers are wrapped around the loop and your fingers point in the direction of the current, your thumb (pointing upward, hitchhiker style) will be pointing in the direction of the field inside the loop. That would be out of the page in
Figure (1c).

At the center of the circular loop, this field is normal to the loop and has a magnitude of

( 1 )

B_loop =

μ₀NI

where μ₀ = 4π × 10^–7 T · m/A (the permeability of free space), N is the number of turns or loops, I is the current (amps), and r = 0.20 m (the radius of the loop). This equation assumes that the N turns make up a flat coil (think Saturn's rings) and that all turns are of the same radius (think Saturn's rings merged into one ring of radius r). Since this would require that the turns actually coincide, which is impossible, the equation is only approximate and most accurate with a small number of thin, closely packed wires. That is the case with our apparatus. The term NI gives the total current around the loop since each turn individually contributes a current, I, to the total current around the loop. We're going to investigate the magnetic field at the center of a circular loop with 1–5 turns. Since the north end of a small compass will point in the direction of the net magnetic field at its location, we can use it to indicate the net field at the center of our loop. Figures (2a)–(2c) illustrate a simple version of our apparatus seen at two glancing angles and one view, (2c), from overhead. The white card in each figure sits atop a sheet of glass. A loop of several turns of wire passes through the glass so that half the loop is above the glass and half is below. The compass sits on the glass at the center of the loop. All this is to help you understand Figures (3a)–(3c). All three are overhead views just like Figure (2c). Each figure ((3a)–(3c)) represents a cross section of three turns of wire represented by the three pairs of dashed lines connecting the three horizontally aligned pairs of circles. The circles represent cross sections of wires passing through the glass sheet supporting the compass. The dashed lines represent the semicircular sections of wire above and below the glass plate. In Figures (3b) and (3c), the dots (•) and crosses (×) indicate currents flowing upward, out of the page, and downward, into the page, respectively. The arrows in the plane of the page all indicate horizontal, parallel to the glass sheet, magnetic fields.

Figure 2: A Compass at the Center of a Current Loop

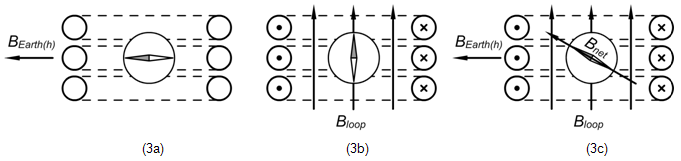
So we have a compass at the center of the loop to detect the magnetic field produced by the current. But there's a bit of a complication. The compass actually detects the net field, B_net, and the net field depends on the contributions of the loop's field and Earth's (actually, just the horizontal component of Earth's field, B_Earth(h)).

Figure 3: The Magnetic Field at the Center of a Current Loop

Figures (3a)–(3c) show the three possibilities: the horizontal component of Earth's field only, the loop's field only, and both of these plus their resultant, B_net, indicated by the compass needle. Actually, the compass indicates B_net in all three figures. We want to begin by investigating the loop's field shown in Figure (3b), but we can only produce the fields shown in Figures (3a) and (3c)! The reason is that we can observe the current off situation, which is (3a), and the current on situation, which is (3c), but since we don't have a way of turning off or shielding against Earth's magnetic field, we can't see the just the loops field, which is (3b). We'll have to be creative to find the field B_loop. Think about it. The field in (3a) plus the field in (3b) equals the net field in (3c). To find the unknown field in (3b), we just need to subtract! But, it's vector subtraction. We can describe Figure (3c) by the vector equation.

( 2 )

B_net = B_loop + B_Earth(h)

Figure 4 is a vector diagram of Figure (3c). You should be able to see how it's generated from equation 2 as well as how it describes the fields in Figure (3c).

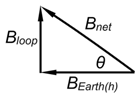
Figure 4: Net Magnetic Field

From Figure 4, we can say

( 3 )

tan(θ) =

B_loop

B_Earth(h)

Explore the Apparatus

We'll use our virtual Tangent Galvanometer to study this interaction between Earth's field and the loop's field. The apparatus is viewed from two perspectives, as shown in Figure 5: View 1: Overhead and View 2: Oblique. You'll switch between views using the button at the top left corner of the screen. The oblique view shown in Figure (5b) provides the best view of the apparatus. Click the "View" button to choose "View 2: Oblique." A frame attached to a rotating table supports a circular loop made of insulated wires. From 1 to 5 turns are possible. A horizontal platform holds a sheet of polar graph paper used for measuring angles in the horizontal plane. There is also a small compass located at the center of the paper. The compass is also at the center of the circular, current-carrying wire loop. Switch to "View 1: Overhead." In the overhead view shown in Figure (5a), you see two vector arrows. The almost horizontal blue one represents the horizontal component of Earth's magnetic field. The almost vertical orange one represents the magnetic field produced by the current-carrying wire loop. It's only visible when that field is present, that is, when the loop current is turned on. Neither vector automatically points in the appropriate direction. Rather, these vectors can be rotated as needed by dragging the heads (tips) of the arrows. Try it now to reinforce that you have this task to perform. More instructions on this follow. In overhead view, the entire apparatus can be rotated by dragging the Handle. The loop field vector arrow, B_loop, rotates with the apparatus. But you can rotate it relative to the apparatus by dragging its head as previously discussed. B_Earth(h) does not rotate with the apparatus. Can you see why? Again, you are responsible for orienting these vectors in the proper directions. The two views are completely independent. You'll only work with one view while performing a given part of the lab. You'll use the overhead view for Part I of the lab and the oblique view in Parts II–III.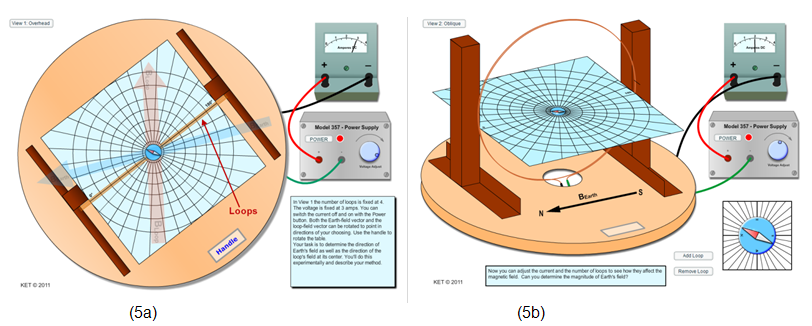

Figure 5: Tangent Galvanometer Views: (a) View 1: Overhead (b) View 2: Oblique

Take some time to become familiar with each view. Explore the following in the oblique view.

a
Notice how the large compass at the bottom right provides a close-up of the "real" compass. You'll take compass readings with this large version. The red end is its north end, so it points in the direction of the net field at the center of the loop.
b
Notice how the deflection of the compass is affected by the power switch, the voltage adjust knob, and the number of turns of wire. Be sure to try all three.
c
When the power is on, the current in the loop produces a magnetic field similar to the one shown in Figure (1b) except in three dimensions. We're only interested in the field at the center of the loop where the compass is located. We expect it to be normal to the plane of the loop but will ultimately prove this. If Earth's magnetic field were nonexistent, the compass needle would point in the direction of the loop's field. However, under the influence of the two magnetic fields, the compass takes the direction of their resultant field, B_net.
d
Note the important relationship between the two fields given in equation 3
tan(θ) =
B_loop
B_Earth(h)
.
. The tangent of θ is directly proportional to B_loop. (B_Earth(h) is constant.) In this lab, we will use the reverse of this (i.e., that B_loop is proportional to tan(θ)).
e
As stated in the Purpose, we'll use the apparatus to test and/or determine the following.

In Part I, we'll explore the addition of magnetic fields and verify that the field at the center of a current loop is normal (perpendicular) to the loop and in accordance with our right-hand rule for the field at the center of a loop.

According to equation 1

B_loop =

μ₀NI

, the field at the center of the loop is determined by the number of turns on the loop, N, and the current in the loop, I. Thus, the field is determined by the product, NI. We'll test this relationship between B and NI in Part II.

III

From a graph of tan(θ) vs. I, we'll determine the experimental horizontal component of Earth's magnetic field, B_Earth(h), at the virtual location of the apparatus. Note that our apparatus behaves as if it were at a specific location on Earth. You'll learn that location later. We'll use B_Earth(h) and the inclination (dip angle) at the location of the apparatus to find the experimental total value of Earth's field, B_Earth, at the location of our apparatus and compare it to the actual value.

Procedure

Please print the worksheet for this lab. You will need this sheet to record your data.

I. Addition of Magnetic Fields at the Center of a Current Loop

You'll use the overhead view for this part of the lab. In this view, the number of turns is fixed at 4, and the current is fixed at 3.0 A when the power is turned on. Begin with the power turned off.

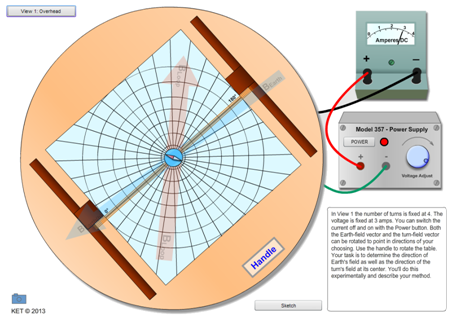
Figure 6: View 1: Overhead

As described earlier, Earth's field is omnipresent in this lab, so you'll need to keep track of its direction. You'll now find Earth's field's direction and align the B_Earth(h) vector with it to use as a fixed reference. So how do you find the direction of Earth's field?

a
A compass will always point in the direction of Earth's magnetic field. True or false?
b
A compass will always point in the direction of the net magnetic field. True or false?

So we can use the compass to find the direction of Earth's field, but we'll have to make sure that the current is off so that we're seeing just the one field.

Whoa! Sorry for the interruption, but two coworkers just came into my office for coffee. They both picked up tiny compasses from a collection I had spread all over a table. Lots of "ooh's" and "ahh's" and "can I keep this's." Then they asked how you work them. I explained to them what most people don't know and that's if you rotate the compass body so that the "N" is under the (usually) blue or red end of the balanced magnetic "needle," everything else on the compass body points in the correct direction.

Figure (7a)

So when you pick up a compass, it might be oriented like Figure (7a) with the needle aligned with the NW direction. But the compass needle actually (with no competing fields) points magnetic north.

Figure (7b)

So if you rotate the compass body counterclockwise until it's aligned as in Figure (7b), west is to your left, etc. Now you can use it to navigate. That's what you need to do now. You need to set up your apparatus to behave like a compass. Incidentally, cheap compasses like these are just as likely to have their ends reversed. The orientation of their domains is easily changed by the presence of nearby magnets.

Just as when my coworkers picked up the compasses, your apparatus starts out at some random angle relative to where it needs to be in order to be useful. Since only Earth's field is present, the (red) end of the compass is now pointing north. Drag the table's Handle until the polar graph paper is aligned so that 0° corresponds to north. This should be to the left. Now you can align the B_Earth(h) vector with Earth's magnetic field at the virtual location of your apparatus. Do this by dragging the head of the B_Earth(h) vector to point in the magnetic north direction. You'll want to keep that vector right where it is since it represents the one thing you can count on. You can rotate the table or turn the current on and off, and the B_Earth(h) won't budge. Earth's field is fixed. Or is it? For this part of the experiment, you can count on it as fixed, but, as you'll see at the end, it does tend to wander off!

North is now to the left of your screen. What direction is east on your screen? Get yourself oriented to these cardinal directions on the table.

Now for a puzzle: We want to investigate the direction of the field produced by the current loop. Specifically, we want to study the field at the center of the loop. How can you do that when Earth's field is always present? Any ideas? A solution is not really obvious to most students. It helps if you first gain some practice dealing with dynamic magnetic fields as opposed to the static ones in your textbook. Let's start by assuming that the loop's field is actually normal to the loop and look at several arrangements to see how Earth's field and the loop's field interact. Look back at Figure 4. In this case, the fields were at right angles. But you can do a similar vector addition regardless of the angles. But it will only be approximate since you don't know the magnitudes of either field. The lengths of your vectors will just be guesses, but they will keep the same length since we'll keep the current fixed and Earth is pretty trustworthy.

Figure 4R: (Revised)

Turn on the current. The compass will most likely deflect to look somewhat like Figure 4R. With the Handle, rotate the table slowly a few times and watch the compass. It moves very strangely—gradually turning and then snapping to a horizontal position before sort of repeating the process but with different ranges of magnitudes. Then it starts over. Let's try something more orderly. Orient the table so that 0° is again to the north. There's a B_loop vector that can be rotated just like the B_Earth(h) vector. You can adjust it, but unlike the B_Earth(h) vector, it rotates with the table. Since we're assuming that B_loop is normal to the loop, the B_loop vector is either east (up) or west (down). Let's try east. Drag the head of the B_loop vector to point in that direction. Turn the current off to display just B_Earth(h). Now turn on the current to add B_loop. You can now see the correct directions of B_Earth(h) and B_net, along with your assumed direction for B_loop. You have no magnitudes to work with, but if you're correct about the direction of B_loop, the vector diagram would look something like Figure 4R. The angle, θ, looks to be a bit less than 40°. Zooming in helps.

Turn on Sketch and create a vector diagram like Figure 8. (Don't worry about the labels yet.) Drag the B_loop and B_Earth(h) vectors onto the apparatus with the tail of each at the center of the compass as shown in Figure 4R. Zooming helps. Drag the head of each in the appropriate direction and make B_Earth(h) somewhat longer than B_loop since the angle, θ, was less than 45°. Making them 5 and 4 radial units long, respectively, works pretty well. (That is, the radii of the 5th and 4th concentric circles.) Drag the two vectors back to the sketching area, add them tail to head as in Figure 4, and then adjust B_net to show their vector sum. Use the label tool to label each vector. You should have a figure much like Figure 8.

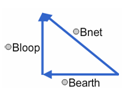
Figure 8: Sketching Vectors

In what follows you'll need to access the "Power Supply," which is covered up by the Sketch area. Use the Sketch button to show and hide the Sketch area as needed. Avoid using Clear Sketch. It's better to just reuse vectors. Your figure should be pretty convincing evidence that B_loop is perpendicular to the loop as we've assumed. But it would also be pretty convincing evidence for the argument that B_loop is, say, 10° clockwise or counterclockwise from being normal to the loop. Picky? Have you noticed how bizarre magnetism is? So we haven't confirmed our guess at the direction, but it's certainly true that B_loop could be normal to the loop.

Let's try a couple of predictions. Imagine the effect of rotating the loop 45° counterclockwise of its "handle down" position. (See the little snapshot for guidance.) In Figure (9a), sketch with a pencil a vector diagram showing your prediction of the addition of B_loop and B_Earth(h) for this arrangement.

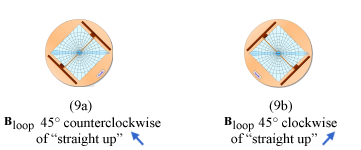
Figure 9

Turn on the current. Change the coil's direction by rotating the table 45° counterclockwise. Notice that the B_Earth(h) vector stays put as it should, but our assumed B_loop vector rotates with the table. It now "points" (magnetic) northeast. Also the lengths of both these field vectors should remain the same as before.

Turn the current off and on. The behavior of the compass needle should make sense. In what direction, relative to the B_loop and B_Earth(h) vectors, does the compass needle point when current is flowing, and why does this make sense for this situation?

Turn the current off and rotate the loop 45° clockwise of its "handle down" orientation. (See snapshot.) In Figure (9b), sketch with a pencil a vector diagram showing your prediction of the addition of B_loop and B_Earth(h) for this arrangement.

For the next two steps, rotate the coil and turn the current on and off as needed to create two diagrams using Sketch. Add vector labels as shown in Figure 8.

Turn Sketch back on and record what you've observed in Figure (9a) by drawing a vector diagram. The best way to do this is to drag your vectors back onto the table and change their directions as necessary, but not their lengths. Take a Screenshot

and upload it as "TG_I_Fig1".

Repeat for Figure (9b). Take a Screenshot and upload it as "TG_I_Fig2".

Which B_net is greater, (9a) or (9b), and why?

Let's try a different scenario. In Figures (10a) and (10b), again without the use of the apparatus, sketch two new vector diagrams showing the addition of B_loop and B_Earth(h), first when the loop has been rotated 90° counterclockwise (of its "handle down" orientation) and then 90° clockwise. Again see the little snapshots for guidance.

Figure 10: (10a) B_loop 90° counterclockwise of "straight up" (10b) B_loop 90° clockwise of "straight up"

Try it. Return the coil to its initial "handle down" orientation. Turn on the current. Change the coil's direction by rotating the table to 90° counterclockwise of the initial setting.

Turn Sketch back on and record what you've observed in Figure (10a) by creating a labeled vector diagram. Be sure to think about what, if anything, happens to the lengths of B_loop and B_Earth(h). Take a Screenshot and upload it as "TG_I_Fig3".

Repeat for Figure (10b). You'll need to rotate the coil 180° from where you left it in the previous step. Take a Screenshot and upload it as "TG_I_Fig4".

We started off by assuming that B_loop was normal to the plane of the loop but had no proof because we didn't know any magnitudes. But these last two figures can be used to prove that B_loop is normal to the loop. You should be able to use some insights that you've gained from the diagrams above to explain how either of our last two figures can be used to prove this point. Here's a hint: For the five arrangements you've drawn diagrams for, think about what happens in each case when you turn the current off and on. It's different for these last two cases. What's the evidence and how does it prove that B_loop is normal to the loop?

We now know that B_loop is normal to the loop, but that allows for two possible directions. Which one is it? There are several drawings that you've produced that could be used to answer this question. Pick one and explain how it provides the answer.

One final question: What about the direction of the current in the loop? With the initial "handle down" setting, is the current flowing into the screen at 180° (the south end) or 0° (the north end)? Explain using your right-hand rule for the field at the center of a current loop.

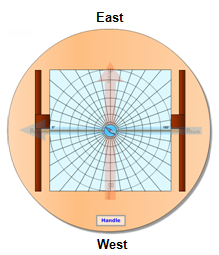
Figure 11: The Direction of the Current in the Loop

II. Confirm That the Magnetic Field at the Center of a Circular Loop Is Directly Proportional to the Number of Loops, N, and the Current, I

We would now like to investigate the effect of the number of loops, N, and the current, I, on the magnetic field at the center of a current loop as described by equation 1. We can't measure B_loop directly, but we can get around that by using equation 3.

( 1 )

B_loop =

μ₀NI

( 3 )

tan(θ) =

B_loop

B_Earth(h)

After combining equations 1 and 3, we have

( 4 )

B_Earth(h) tan(θ) =

μ₀NI

Since B_Earth(h), μ₀, and r are constants, we can say that

( 5 )

tan(θ) ∝ NI.

So if equation 1 is correct, tan(θ) should be directly proportional to N and to I. Thus, we can confirm that B ∝ N and B ∝ I by plotting tan(θ) vs. N for a constant current, and then plotting tan(θ) vs. I for a constant number of turns, N. Straight lines for each plot would confirm the relationship. You'll use the oblique view this time.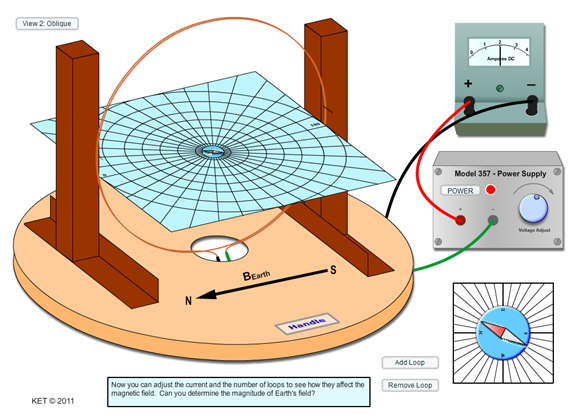

Figure 12: Oblique View

You'll make your measurements using the large close-up view of the compass at the bottom right of the screen. You'll need to read the compass as accurately as possible. Zooming in is very useful here. Just right click (Ctrl+click on a Mac) on the compass and select "Zoom In" from the menu.

To test the effect of N on B_loop, measure the angle of deflection (with respect to north) of the compass for 1–5 turns. Use the Add Turn and Remove Turn buttons. N is initially set to 3. Use a current of 3 A.

Record your results in Table 1 and calculate tan(θ) for each value of θ.

Test your results by entering your data in Grapher and using it to plot a graph of tan(θ) vs. N. Take a Screenshot of your graph and upload it as "TG_tanTheta_N". You can turn on all three graphs to reduce the size of the graph.

Sketch your graph on the grid in Figure 13.

Figure 13: tan(θ) vs. N

Does your graph indicate that tan(θ) is directly proportional to N? How? (Two criteria are required to indicate a direct proportion. See the introductory materials if you need a review.)

To test the effect of the current on B_loop, measure the angle of deflection for currents of 0 to 3.5 A in 0.5-A increments. Use 5 turns for this step.

Record your results in Table 2 and calculate tan(θ) for each value of θ.

Test your results by plotting a graph of tan(θ) vs. I in Grapher. Take a Screenshot of your graph and upload it as "TG_tanTheta_I".

Sketch your graph on the grid in Figure 14.

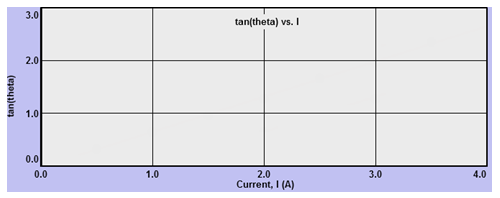
Figure 14: tan(θ) vs. I

Does your graph indicate that tan(θ) is directly proportional to I? How? (Two criteria are required.)

III. Experimentally Determine the Horizontal Component of Earth's Magnetic Field at the Location of Your Virtual Apparatus and Compare It to the Actual Value There

The magnetic field of the Earth varies in magnitude and direction in time and space. That is, everywhere you go, it's different. And it changes from day to day at each location! Your apparatus is reacting to Earth's field, so it's obviously somewhere. The virtual location of your apparatus for this experiment is Hamilton, Bermuda. That is, it behaves as if it were at that location. You'll now use the data that you've already taken "in Hamilton" and compare it to the actual value at that location. We now know from equation 1

B_loop =

μ₀NI

that B_loop is directly proportional to NI. And from equation 3

tan(θ) =

B_loop

B_Earth(h)

, we know that B_Earth(h) is directly proportional to B_loop. So we can use these two equations together to calculate B_Earth(h) in Bermuda. We can then compare it to the actual value at that location. We'll do that as follows.

a
Using a point from the line of best fit (not a data point) on your tan(θ) vs. I graph, calculate B_loop for the current at that point on the graph using equation 1.
b
Compute your experimental value B_Earth(h) (in Bermuda) using equation 3.
c
Find the actual value of B_Earth using resources provided at NOAA.gov.
d
Calculate the actual value of B_Earth(h) from the actual value of B_Earth using trigonometry.
e
Compare your experimental value for B_Earth(h) to the actual value.

Using your tan(θ) vs. I graph, turn on "Interpolate" in Grapher. As you move your pointer (without dragging) across the graph, a ring and vertical line will follow your pointer horizontally. As your pointer moves, the current and tan(θ) values for each point on the plotted line will appear in the "Interpolate" text box. Using a convenient point on your line of best fit, determine the loop's magnetic field, B_loop, using equation 1. Record I and tan(θ) for your chosen point along with your calculations. Note that r = 0.20 m for our loop.

Using equation 3

tan(θ) =

B_loop

B_Earth(h)

and the value of tan(θ) from your chosen point on your graph, calculate the experimental horizontal component of Earth's magnetic field, B_Earth(h). Show your calculations.

You now have your experimental value for the horizontal component of Earth's magnetic field in Bermuda. You'll now use a government resource to find the actual value of B_Earth at that location. Then, so that you can compare it to your experimental results, you'll need to compute B_Earth(h). Let's see how these two values are related. In the northern hemisphere (where the apparatus is located), the field dips down into the Earth, as shown in Figure (15a). B_Earth is the actual, total magnetic field at Earth's surface at this location. It has a horizontal (tangent to Earth) component, B_h, and a vertical component, B_v, as illustrated in Figure (15a). The angle of inclination, or dip angle, θ_dip, is the angle between the horizontal component, B_h, which we've been working with, and the total field, B_Earth. Figure (15b) is another version of Figure (15a) intended to clarify the geometry.

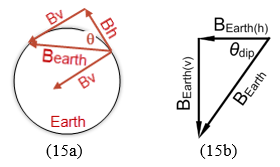
Figure 15: The Dip Angle

If we knew B_Earth and the dip angle at the location of our apparatus, we could compute the actual value of B_Earth(h) using trigonometry. We'll do that next. But to get the hang of it, let's check it for your house.

Navigate to NOAA's National Centers for Environmental Information. Use "Lookup Latitude/Longitude" in the right column. Enter your zip code and click "Get & Add Lat/Lon." You'll see your latitude and longitude in the left column. N and W were automatically selected since the code behind this site knows that from your zip code. These indicate north or south of the equator and east or west of Greenwhich. These values can be provided in one of two formats—degrees, minutes, and seconds or decimal degrees. Here's an example of these two formats. They are nowhere near the values you find in this lab.

Example latitude: 25° 12' 50'' N or 25.2139° N

There will also be a longitude in a similar format. Now click "Calculate" near the bottom of the page. A pop-up window will appear with a set of numbers for your location. The last one on the right, the "Total Field," is what we're calling B_Earth. It's in nanoTeslas, nT. Once you've had a look at the data for your location, click the close icon on the pop-up window.

Back to Bermuda! Under "Lookup Latitude/Longitude," choose Bermuda for Country and Hamilton for City. Click "Get & Lat/Lon." Record the latitude and longitude in Table 3 in either degrees, minutes, and seconds or decimal degrees format.

Click "Calculate." From the pop-up window, record the "Total Field," B_Earth, for Hamilton. Note the nT units. You'll need to convert that to Teslas in standard format scientific notation (#.#### × 10^–5 T).

Record the inclination (dip angle) in Table 4. Your calculator is probably not comfortable with degrees, minutes, and seconds. You need to convert this angle to decimal degrees. There's a tool online to do this conversion at https://www.fcc.gov/media/radio/dms-decimal to convert to decimal degrees. You'll figure it out. Record the result.

From the current actual total field, B_Earth, and dip angle, you can determine the current actual value of B_Earth(h). You can figure this one out on your own using Figure 15. Show your calculations of the actual value for B_Earth(h).

Calculate and record the percentage error between your actual and experimental values for B_Earth(h).

Return to the NOAA.gov site and bring back the pop-up window with all the data in it. You'll see that the "Horizontal Intensity" is provided. Does that look familiar?

One last thing. Note the row labeled "Change/Year." If you come back to this table in a month or so, or even next week, the numbers will be different. In the spring of 2013 the values were the following.

Total Field (Intensity) (B_Earth)	4.537 × 10^–5	T	in spring of 2013
Inclination (dip angle)	56.84	°	" "

Earth's field is always changing! Who cares? Here's an optional, very cool, side trip to find out who cares. Listen to the podcast about research on how sea turtles adjust to this change: http://www.sciencefriday.com/segment/01/16/2015/sea-turtles-guided-home-by-magnetic-sense.html.